数据挖掘方法之二：回归模型（简单线性回归）

注：文中所使用代码为R

一概念

简单线性回归模型是用于估计一个连续预测变量和一个连续回应变量的线性关系。回归方程或估计回归方程(estimated regression equation,ERE)：
$$\bar y=b_0+b_1x$$

$\bar y$是回应变量的估计值
$b_0$是回归线在y轴上的截距
$b_1$是回归线的斜率
$b_0$和$b_1$称为回归系数

二实例

数据来源: 谷物数据集
数据描述：谷物数据集,包含了77种早餐谷物的16个属性对应的营养信息
首先导入数据：

1	sugar<-read.table(file="/LabData/RData/regression/nutrition.txt",header=TRUE)

部分数据概览如下：

edit（sugar）

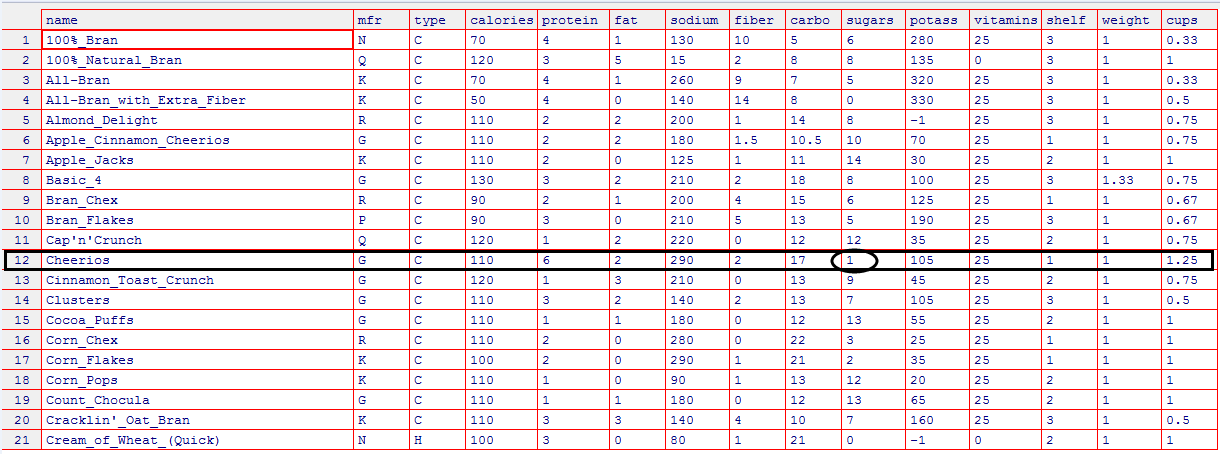
就给定谷物的含糖量对该谷物的营养成分进行评价，77种谷物的营养级别与含糖量的散点图和拟合回归线如下:

    plot(data=sugar,rating~sugars,main="营养级别和含糖量的散点图及拟合线",xlab="含糖量",ylab="营养级别")  

    lm.reg<-lm(data=sugar,rating~sugars)  

    abline(lm.reg,lty=4,lwd=3)   
```  
![拟合](/images/blog/regression2.png)

使用线性回归模型拟合结果如下：

lm(data=sugar,rating~sugars)       
Call:      
lm(formula = rating ~ sugars, data = sugar)      
Coefficients:      
  (Intercept)       sugars        
   59.284       -2.401

这里给定ERE为 ： $\bar y=59.284-2.401*sugars$， 所以$b_0$=59.284,$b_1$=-2.401   

### 误差残留   

 **问题**：数据集中包含了一个含糖量(sugars=1)为1的谷物 cheerios(数据概览中，黑色框部分)，其营养价值是50.765,而非估计值的56.98.
  二者之差也即

$$y-\bar y=56.98-50.765=6.215,$$

称为预测误差(prediction error)、估计误差(estimation error)或者误差残留(residual error)。

为寻求这种预测误差总体尽可能小，最小二乘回归法会选择一条唯一的回归线，满足使得数据集的整体残差平方和达到最小值。有多重方法可以选择，如中位数回归方法，但最小二乘法回归是最常见的。   
<br>

## 三 误差评估

### 1 最小二乘法估计   

公式如下：

$$y=m_0+m_1x+e$$
   <font color="blue">其中误差项e引入用以解释不确定性的因素。</font>

**基本假设**

1. 零均值假设：误差项是期望为零的随机变量，即$E(e)=0$
2. 不变方差假设：误差项e的方差（用$σ^2$表示）是常数且与 $x_1,x_2,....$ 的值无关
3. 独立性假设：e的变量是相互独立的
4. 正态性假设：误差项e是正态随机变量,也即：误差项e的值是独立的正态分布随机变量，带有均值0和不变方差$σ^2$

回应变量y的分布:

(1)根据零假设，回应变量y的值均落在回归线上
(2)根据不变方差假设，不论预测变量x1,x2,..取什么值，y的方差不变
(3)根据独立性假设，对任意的 $x_1,x_2,..$ 取值，y的值都是相互独立的
(4)根据正态性假设，回应变量y也是正态分布的随机变量。也即回应变量y也是独立正态变量，均值不变，方差不变。
最小二乘回归线(least-square line)将误差的平方和最小化，总的预测误差用SSEp表示，则总的误差平方和为：

$$
   SSE_p=\sum^n_{i-1}\epsilon^2=\sum^n_{i-1}(y_i-\beta_0-\beta_1x_i)^2
$$

利用微积分，在以下微积分方程结果为0的时候, $b_0$ 和 $b_1$ 的取值会让总的误差平方和最小。关于 $b_0$ 和 $b_1$ 的偏微分方程为:

$$
   \frac {\partial SSE_p}{\partial \beta_0}=-2\sum^n_{i-1}(y_i-\beta_0-\beta_1x_i)
$$

$$
   \frac{\partial SSE_p}{\partial \beta_1}=-2\sum^n_{i-1}x_i(y_i-\beta_0-\beta_1x_i)
$$

令上式为0，则有:<br>
$$
(y_i-\beta_0-\beta_1x_i)=0
$$

$$
(y_i-\beta_0-\beta_1x_i) =0
$$

分别求和，得到

$$
  \sum^n_{i-1}y_i-nb_0-b_1\sum^a_{i-1}x_i=0
$$

$$
   \sum^n_{i-1}x_iy_i-b_0\sum^n_{i-1}x_i-b_1\sum^n_{i-1}x^2_i=0
$$

重新表示为：

$$
  b_0n+b_1\sum^n_{i-1}x_i=\sum^n_{i-1}y_i
$$

$$
   b_0\sum^n_{i-1}x_i+b_i\sum^n_{i-1}x_i^2=\sum^n_{i-1}x_iy_i
$$

求出 $b_0$ 和 $b_1$ 的值：

$$
  b_1=\frac{\sum x_iy_i-[(\sum x_i)(\sum y_i)]/n}{\sum x^2_i-(\sum x_i)^2/n}
$$

$$
  b_0 = \bar y-b_1\bar x (\bar x为x 的均值)
$$


### 2 决定系数

$r^2$ 称为决定系数（coefficient of determination）用来衡量回归线的拟合度，也即最小二乘回归线产生的线性估计与实际观测数据的拟合程度。前面提到y^代表回应变量的估计值，$y-\bar y$ 代表预测误差或残差。

#### 引子

1.想象一下，如果不考虑数据集中含糖量而直接预测其营养价值，我们直观的做法是求其平均值作为预测值。假设开始为数据集里的每个记录计算(y-y')（其中y'为回应变量的平均值），然后计算其平方和，这与计算误差(y-y^)，然后计算误差平方和类似。这时统计量总体误差平方和SST为：

$$
   SST =(y_1-y')^2+(y_2-y')^2+(y_3-y')^2....
$$

SST，也称为总体平方和(sum of squares total，SST)是在没有考虑预测变量的情况下，衡量回应变量总体变异的统计量。

2. 接下来是衡量估计回归方程能多大程度提高估计的准确度。运用回归线时的估计误差为： $y-\bar y$  ,当忽略含糖量信息时，估计误差是 $y-y'$ 。因此改进量是：$\bar y-y'$ .进一步基于 $\bar y-y'$ 构造一个平方和的统计量，这样的统计量被称为回归平方和 *(sum of squares of regression,SSR)* ，是相对于忽略预测信息，衡量在使用回归线后预测精度提高的统计量，即：

$$
   SSR = (\bar y_1-y')^2+(\bar y_2-y')^2+....
$$

由: $y-y'=(\bar y-y')+(y-\bar y)$  两边都进行平方，然后进行总和运算，有：

$$
  SST =SSR +SSE
$$

#### 结论   

SST衡量了回应变量变异的一部分，这部分是被回应变量和预测变量之间的线性关系所解释的。然而不是所有的数据点都正好落在回归线上，这意味着还有一部分y变量的变异不能被回归线所解释。SSE可以被认为是衡量不能被x和y之间的回归线所解释的其他变异，包括随机变异。
决定系数 $r^2$ ，它衡量了用回归线来描述预测变量和回应变量之间线性关系的符合程度

$$
   r^2 =\frac{SSR}{SST}
$$

### 3 估计值的标准误差

**符号**：*S*

**概念**：用于衡量由回归线产生估计值的精度的统计量。
为介绍s，首先引入均方误差 *(mean squares error，MSE)* ：

$$
    MSE = \frac{SSE}{n-m-1}
$$

其中，m标示预测变量的个数，简单线性回归是m=1,多元线性回归时m大于1。与 *SSE* 一样， *MSE* 用于衡量在回应变量中没有被回归分析所解释的变异。
标准误差的估计由下式给出:

$$
   S =\sqrt {MSE}=\sqrt {SSE/(n-m-1)}
$$

 *S* 值为“典型”残差的估计，*s* 是衡量估计中的典型误差，即回应预测值与实际值之间的差异。也即标准误差能反应估计回归方程做出预测的精确度，因此 *s* 越小越好。

### 4 其他评估   

#### 1. 相关系数

用来定义两个变量线性关系的统计量称为相关系数 *(correlation coefficient，也称皮尔森相关系数)* ，用来衡量变量之间线性关系强弱。计算公式如下：

$$
   r =\frac{\sum (x-x')(y-y')}{(n-1)S_xS_y}
$$

+ 其中 $S_x$和 $S_y$分别代表样本x和y的标准差
+ 相关系数r的取值范围为：(-1,1)
+ 变量r的值越接近于1，表明二者正向相关性越大，随着x增大y也会增大。
+ 变量r的值越接近于-1，表明二者负向相关性越大，随着x增大y会减小。

#### 2. 方差分析表(ANOVA table)   

一般形式如下：

|变异源|平方和( *SS* )|自由度|均方差( *MS* )|F|
|---|---|---|---|---|
|回归| *SSR* | *m* | $MSR =\frac{SSR}{m}$ | $F= \frac{MSR}{MSE}$ |
|误差| *SSE* | *n-m-1*| $MSE =\frac{SSE}{n-m-1}$ ||
|合计| *SST=SSR+SSE* | *n-1* |||

下面展示了 糖含量营养级别回归结果:

anova<-aov(data=sugar,rating~sugars)
summary(anova)
Df Sum Sq Mean Sq F value Pr(>F)
sugars 1 8655 8655 102.3 1.15e-15
Residuals 75 6342 85

sugars      ***  
Residuals        
           ---

Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1



#### 3. 异常点、高杠杠点和强影响观测值   

 **高杠杆点** *(High leverage point)*：可以被认为是一个观测值在预测空间中的极限，也即一个高杠杆值可以被认为是不考虑y值得x变量的极限。杠杆第i个观察值hi可以被标示如下（x'为平均数）：

 $$
   h_i =\frac{1}{h}+\frac{(x-x')^2}{\sum (x_i-x')^2}
 $$

对于给定数据集,1/n和右边分式分母都是常数，所以第i个观察的杠杆只依赖于 $(x_i-x')^2$。
一个拥有大于 $\frac{2*(m+1)}{n}$ 和 $\frac{3*(m+1)}{n}$ 的观察点被认为是高杠杆点。

**异常点** 观测到的偏离回归直（曲）线的点。一种粗略的评价观察值的方法是使用标准残留值 *(standardized residuals)*一般用:

$$
   S_{i,resid}=s\sqrt{1-h_i}
$$

来标示第i个残留数的标准差，则hi代表第i个观测值的杠杆影响，那么标准残留值可以表示为:

$$
    r_{i,stand }= \frac{(y-y'_i)}{s_{i,resid}}
$$

如果标准残留值得绝对值超过了2，就可以认为是一个异常点,上图中观测点1和4应该是异常点。

 **强影响力点** ：对数据集的分析造成较大影响的观测点。通常强影响力观测值同时有较大的残留值和较高的杠杆，但也有可能它既不是异常点也没有较高的杠杆，但两者特点组合成一个具有影响力的点。粗略估算一个观察点是否是强影响力点的方法是看它的Cook距离 *(Cook's distance)* 是否大于1.0，更确切的说，用Cook距离与F分布 *(m,n-m)* 来比较，若观测值落在分布的第一部分（低于25个百分点），就说它对整体分布只有一点点影响，若落在中点以后就说明该点是有影响力的。Cook距离将残留值和刚刚都考虑进去的，第i个观察点的距离可以为：

$$
   \frac{(y_i-y'_i)^2}{(m+1)S^2}\frac{h_i}{1-h_i}
$$

其中 $y_i-y'_i$表示第i个残留值，m表示预测变量的个数，s为标准误差的估计，hi为第i个观察点的杠杆。左边的比率含有一个元素代表了残留值，右边的函数代表了杠杆值。


## 四 回归推断

最小二乘法回归是建立在一个假设基础上的线性回归模型，我们需要一个系统地框架来评估两个变量之间是否存在线性关系。对于最小二乘法的公式：

$$
     y = m_0+m_1x+e
$$

主要有以下四种方法：

1.用来推断回应变量与预测变量之间关系的t检验法
2. 斜率m1的置信区间
3. 在给定一个特定的预测值条件下，回应变量<B>均值</B>的置信区间
4. 在给定一个特定的预测值条件下，回应变量<B>随机值</B>的预测区间

### 4.1 x和y之间线性关系的t检验

对于简单线性回归t检验与F检验是等价的。<br>

#### 对斜率的估计

用最小二乘法估计的斜率m'(注意m1是真实斜率)是一个统计量，像所有统计量一样服从一个特定均值和标准差的样本分布.斜率的回归推断是基于m'的样本方差的点估计 Sm',Sm'被解释为对斜率变异性的衡量指标，较大的Sm'预示着斜率m*的估计是不稳定的。t检验基于统计量 $t=(m'-m_1)/Sm'$ ,它服从一个自由度为 $n-2$ 的t分布，当零假设为真（变量x和y之间不存在线性关系）时，检验统计量 $t=m'/Sm'$ 服从一个自由度为 *n-2* 的 t 分布。

我们重新概览下77种谷物数据中营养级别与含糖量的线性回归结果：

 lm.reg<-lm(data=sugar,rating~sugars)  
 summary(lm.reg)  

Call:  
lm(formula = rating ~ sugars, data = sugar)  

Residuals:  
    Min      1Q  Median      3Q     Max   
-17.853  -5.677  -1.439   5.160  34.421   

Coefficients:  
            Estimate Std. Error t value Pr(>|t|)      
(Intercept)  59.2844     1.9485   30.43  < 2e-16 ***  
sugars       -2.4008     0.2373  -10.12 1.15e-15 ***  
---  
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1  

Residual standard error: 9.196 on 75 degrees of freedom  
Multiple R-squared:  0.5771,    Adjusted R-squared:  0.5715   
F-statistic: 102.3 on 1 and 75 DF,  p-value: 1.153e-15


我们可以得到：
  + 在系数列下面，找到斜率m'的估计值为 -2.4008。
  + 在SE系数列里找到斜率m'的标准差Sm'为 0.2373
  + 在T值列找到t的统计量，即t检验的值 , $t=\frac{m'}{Sm'}=\frac{-2.4008}{0.2373}=-10.1171$
  + 在最后一列可以找到t检验的p值，是一个双尾检验，形式为：p值= $P(|t|>tobs)$ ，其中的tobs代表观测值。此处P值= $P(|t|>tobs)=P(|t|>-10.1171)$ 近似为0，小于任何显著性要求的合理界限，因此可以拒绝零假设也即认为含糖量和营养级别之前存在线性关系。

### 4.2 回归直线斜率的置信区间

置信区间也即在一定概率P下保证变量落在某区间 [a,b]内。对于回归直线的真实斜率 $m_1$来说，*100\*(1-c)%* 的置信区间也即有 100*(1-c)%的把握保证回归线的真实斜率位于 [ $m'-(t_{n-2})(Sm'),m'+(t_{n-2})(Sm')$ ]区间。其中 $t_{n-2}$ 是自由度为n-2的 t 分布。

例如构建一个回归直线的真实斜率 $m_1$的95%的置信区间。有一个对m1的点估计值 m'=-2.4008,对95%的之心去和自由度为 $n-2=77-2=75$ 的t临界值为 2.0(查表t75.95%=2.0),从表中得到 Sm'=0.2373，因此置信区间为：

$$
    [ $m'-(t_{n-2})(Sm'),m'+(t_{n-2})(Sm')$ ]
$$

相关代码及结果如下：<br>

lm.reg<-lm(data=sugar,rating~sugars)
#level=0.95为置信度
confint(lm.reg,level=0.95)
2.5 % 97.5 %
(Intercept) 55.402783 63.165952
sugars -2.873567 -1.92807


### 4.3 给定x条件下，y均值的置信区间和y随机选择值的预测区间

给定x条件下，y<B>均值</B>的置信区间由如下公式判定：

$$
  \bar y\pm t_{n-2}(s)\sqrt {\frac{1}{n}+\frac{(x_p-\bar x)^2}{\sum(x_i-\bar x)^2}}
$$

其中 $\bar y$ 表示给定x值后，y的点估计值，$t_{n-2}$ 是与样本大小和置信水平相关联的乘数，s是估计的标准误差，$\bar x$ 是产生预测值所对应的x专指变量。

给定x条件下，y随机选择值的预测区间:

$$
   \bar y\pm t_{n-2}(s)\sqrt {1+\frac{1}{n}+\frac{(x_p-\bar x)^2}{\sum(x_i-\bar x)^2}}
$$

 **注意**：第二张图中表达式与第一张图中表达式相比，除了在平方根李出现了 **"1+"** 外完全一样，这说明比起均值估计来，对于单个y值得估计会有更大的变化范围，这也说明了预测区间总是比类似的置信区间要宽

我们希望预测含糖量为 sugars=10时该谷物的营养级别范围，实例代码如下：

> point<-data.frame(sugars=10)  
> point  
  sugars  
1     10  
> lm.reg  

Call:  
lm(formula = rating ~ sugars, data = sugar)  

Coefficients:  
(Intercept)       sugars    
     59.284       -2.401    

> lm.pred<-predict(lm.reg,point,interval="prediction",level=0.95)  
> lm.pred  
       fit     lwr      upr  
 1 35.27617 16.7815 53.77083


可以看到在95%的置信度下，含糖量为10的谷物其营养级别介于 16.7815和53.77083之间

注：文中所使用代码为R

一 概念

二 实例

一概念

二实例