数据挖掘方法之五：逻辑回归

一为何要有逻辑回归

假设有如下关于患者年龄与患病情况的数据集：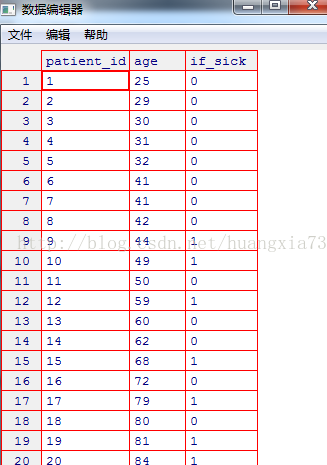

我们查看数据：

> edit(patient)  
        patient_id age if_sick  
   [1,]          1  25       0  
   [2,]          2  29       0  
   [3,]          3  30       0  
   [4,]          4  31       0  
   [5,]          5  32       0  
   [6,]          6  41       0  
   [7,]          7  41       0  
   [8,]          8  42       0  
   [9,]          9  44       1  
   [10,]         10  49       1  
   [11,]         11  50       0  
   [12,]         12  59       1  
   [13,]         13  60       0  
   [14,]         14  62       0  
   [15,]         15  68       1  
   [16,]         16  72       0  
   [17,]         17  79       1  
   [18,]         18  80       0  
   [19,]         19  81       1  
   [20,]         20  84       1  
   > p<-as.data.frame(patient)  
   > plot(p$if_sick~p$age,main="20位患者年龄与患病情况",xlab="年龄",ylab="患病情况")

画出对照图看数据分布：

> plot(p$if_sick~p$age,main="20位患者年龄与患病情况",xlab="年龄",ylab="患病情况")  
> lm<-lm(if_sick~age,data=p)  
> abline(lm)  
> legend(x=65,y=0.2,legend="线性拟合",lty=1)

结果图如下：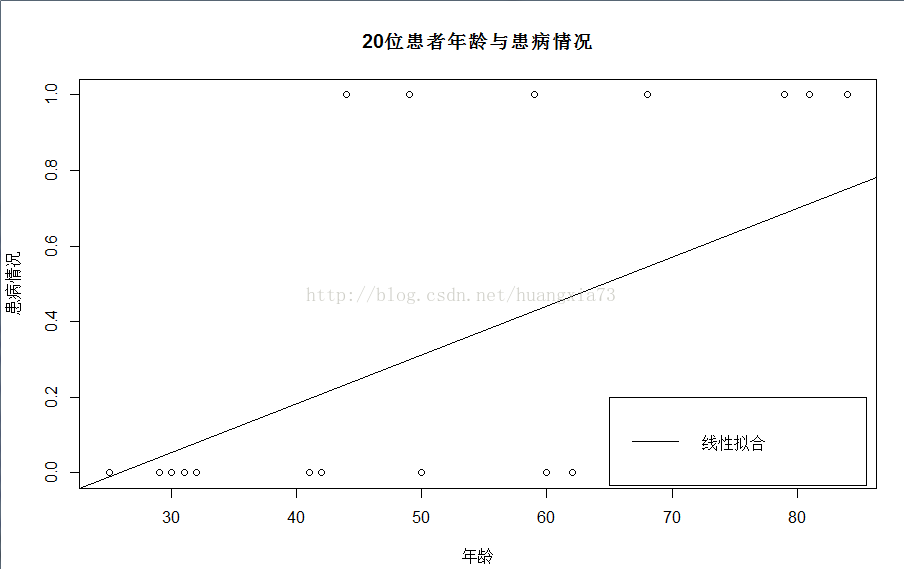

此时，我们发现线性拟合完全偏离了数据分布，即使使用如对数变换也难以取得理想结果，如上图所示数据分布（不是0就是1）提醒我们应该使用逻辑回归。

二 . 逻辑回归概念及认识

2.1 对比线性回归

线性回归是用来估计连续型回应变量与一组预测变量之间关系的方法。

逻辑回归用来估计非连续型（分类型）回应变量与一组预测变量之间关系的方法。

2.2 公式

逻辑回归的条件均值（给定X=x的情况下Y的条件均值表示为：E(Y|x)，以下用π(x)表示）具体如下:

$$
\pi(x)= \frac{e^{b_0+b_1}}{1+e^{b_0+b_1}}
$$

上式形成的图形成为反曲线，是非线性的S型。它的一种逻辑转换如下，它是一种有效的逻辑转换方法：

$$
g(x)=ln\frac{\pi(x)}{1-\pi(x)}=b_0+b_1x
$$

转换函数g(x)表现了线性逻辑回归模型的几个很好的性质，如线性、连续性、取值范围无限性。

取值范围：$\pi(x)在 b_0+b_1x\backsim -\infty 时取最小值0，π(x)在 b_0+b_1x\backsim\infty时取最大值1$ 。

性质：π(x)可以看做一种概率形式，其取值范围为 (0,1).其中

π(x) 可以看做X=x条件下的正效应（如疾病）发生的概率
1-π(x) 可以看做是在这种条件下正效应没有发生的概率。

2.3 误差

线性回归模型中，误差e服从均值为0、方差为常数的正态分布，而逻辑回归由于其回应变量的取值是二分的，其误差只有两种形式：

X=x时，如果出现Y=1的情况，其概率为π(x)，误差为 e=1-π(x)
X=x时，如果Y=0，其概率为1-π(x),误差为 e=0-π(x)=-π(x)

因而，逻辑回归的误差服从二项分布，其方差为π(x)(1-π(x))，这样逻辑回归的回应变量Y=π(x)+e也服从概率为π(x)的二项分布。

2.4 估值（最大似然估计）

最大似然估计：在已经得到试验结果的情况下，我们应该寻找使这个结果出现的可能性最大的那个作为真的估计。

线性回归中使用最小二乘法有可能得到回归系数最优值的闭合形式解，但在逻辑回归中不存在，我们采用的最大似然估计法，得到的观测数据的似然参数估计值是最大的。似然函数 $l(b|x)$ 是一个参数为 $b=b_0,b_1,….$ ，用来表示被观测数据x的概率的函数。在回应变量为正相关的情况下$(X=x_i,Y_i=1)$ ，观测值会影响概率π(x)的值，在回应变量为负相关的情况下 $(X=x_i,Y_i=0)$，观测值会影响概率1-π(x)的值。因此 $Y_i=0或1$，对第i个观测值概率的影响可以表示为 :$[\pi(x_i)]^{y_i}[1-\pi(x)^{1-y_i}]$

假设观测值是独立的，可以把似然函数 $l(b|x)$ 表示为单个项的乘积：$(b|x)=\prod^n_{i=1}$
通过对 $l(b|x)$ 每个参数求微分，并令其微分等于零，可以得到最大似然估计。

2.5 衡量回归模型显著性

先见下表,患病情况与年龄的逻辑回归分析结果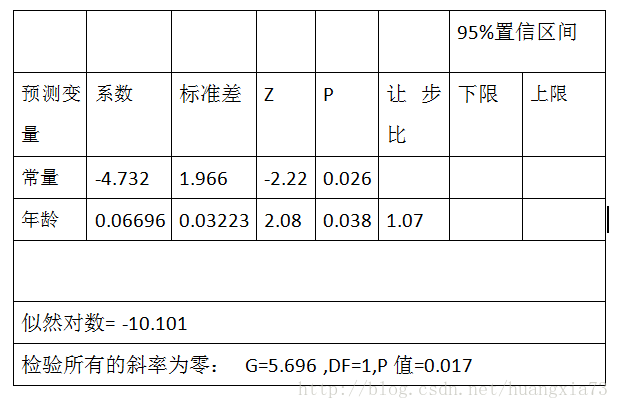

2.5.1 统计量G

在简单线性回归模型中，检验统计量F=MSR/MSE 可以来判断回归模型的显著性。在逻辑回归模型中，检验的是带有某个预测变量的模型比不带该预测变量的模型是否能更好的回应变量匹配。

饱和模型：包含了和数据点个数一样多的参数的模型（能完全正确估计回应变量，没有预测误差）
拟合模型：带有少于数据点个数的参数

偏差定义如下：

$$
偏差 D= -2ln[\frac{拟合模型似然值}{饱和模型似然值}]
$$

上述检验称为似然比值检验，其中-2ln 部分是为了方便计算。将拟合模型中对π(x)的估计值表示为π(x)’，则偏差公式变为：

$$
偏差 D= -2ln\sum^n_{i=1}[y_iln\frac{\pi(x)’}{y_i}+(1-y_i)ln\frac{1-\pi(x)’}{1-y_i}]
$$

该偏差表示考虑了预测变量后模型的误差，它类似于线性回归中的平方和误差。

决定某个特定的预测变量是否重要的程序是计算出不带此预测变量模型的偏差，减去带有此预测变量模型的偏差，即:

$$
G= 偏差(非预测模型)-偏差(预测模型)= -ln[\frac{非预测似然值}{预测似然值}]
$$

统计量G服从自由度为1的卡方分布

在患病情况例子中，从表格可以看到似然对数比是 -10.101，那么:

G=2{-10.101-[7ln(7)+13ln(13)-20ln(20)]}=5.696

2.5.2 Wald检验

该比率为：

$$
Z_{wald}=\frac{b_1}{SE(b_1)}
$$
服从标准正态分布，由表1提供的系数估计值及标准差：b1=0.6696和 $SE(b_1)=0.03223$，于是有: $Z_{wald}=0.6696/0.3223=2.08$

表中P值即为P(|Z|>2.08)=0.038
通常可以为逻辑回归系数构建一个100(1-a)%的置信区间：

$$
[b_0-ZSE(b_0),b_0SE(b_0)]和[b_1-ZSE(b_1),b_1+ZSE(b_1)]
$$

2.5.3 发生比和让步比

发生比：事件发生的概率与不发生的概率的比值。
- 发生比告诉我们一件事情发生或者不发生哪种情况更有可能.一件事情发生的可能性大于不发生的可能性时，发生比大于1。
- 一件事情发生的可能性小于不发生的可能性时，发生比大于1
- 一件事情很有可能发生时，发生比等于1

例如，预测的一个72岁病人换用特定病例的概率为61%，不患此病的概率为39%。因此一个72岁病人患此病的发生比=0.61/0.39=1.56。

让步比：x=1时回应变量发生的发生比除以x=0时回应变量发生的发生比。它很简单的表达了让步比和斜率系数之间的关系

在二分预测变量的二元逻辑回归中，当x=1时，回应变量发生(y=1)的发生比为：$\frac{\pi(1)}{1-\pi(1)}=e^{b_0+b_1}$

相应的，当x=0时，回应变量发生的发生比为：$\frac{\pi(0)}{1-\pi(0)}=e^{b_0}$

则让步比公式如下：

$$
OR= \frac{\pi(1)/[1-\pi(1)]}{\pi(0)/[1-\pi(0)]}=e^{b_0+b_1}/e^{b_0}=e^{b_1}
$$

例如：一个临床试验报告称，曾经使用过与从没有使用过雌性激素替换疗法的人中患子宫癌的让步比为5.0，这可以解释为使用雌性激素替换疗法的人得子宫癌的概率是未使用者的5倍。

一 为何要有逻辑回归