基本概念理解
图像中每个像素都想象成一个神经元
padding: 填充的意思。使用卷积对图像某部分做运算时,总会有部分没有覆盖到,需要决定是否填充以及使用什么填充方式。
stride: 移动切片的步长,影响取样的数量。每次将卷积核(矩阵)在图像上移动时,一次移动的位置量。
局部感知:图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。
其他理解:
- 卷积核心。一个卷积是一个二维矩阵,卷积核心就是矩阵中心
- Patch/Kernel:一个局部切片
- Depth: 数据的深度(通道数),图像数据是三维的,长宽和RGB,神经网络的预测输出也属于一维
- 池化:就是在图像上采样,抽取部分数据。
误差函数
令$y_j(n)$记为在输出层第$j$个神经元输出产生的函数信号。相应的,神经元$j$输出所产生的误差信号定义为:
$$
e_j(n)=d_j(n)-y_j(n)
$$其中$d_j(n)$是响应向量$d(n)$的第$j$个元素。那么瞬时误差能量(instaneous error energy)定义为:
$$
\Im _j(n)=\frac{1}{2}e^2_j(n)
$$将所有输出层误差能量相加,得到整个网络的全部瞬时误差能量:
$$
\Im (n)=\sum {j\epsilon C}\Im(n)=\frac{1}{2}\sum{i\epsilon C}e^2_j(n)
$$其中集合C包括输出层的所有神经元。设训练样本中包含N个样例,训练样本上的**平均误差能量(error energy averaged over the training sample)**或者说经验风险(empirical risk)定义为:
$$
\Im_{av}(N) = \frac{1}{N}\sum^N_{n=1}\Im (n)=\frac{1}{2N}\sum^N_{n=1}\sum_{j\epsilon C}e^2_j(n)
$$epoch 回合
epoch可以理解为回合,一回合代表全部输入数据都走了一遍训练过程,神经网络的训练可能需要经历m个回合。注意:虽然每个回合都是全部输入数据,但是每次输入的组合(即batch组合)是随机的,因为每个batch都是随机从输入样本中抽取固定数量的样本,因而每次的组合各不相同。
padding的类别
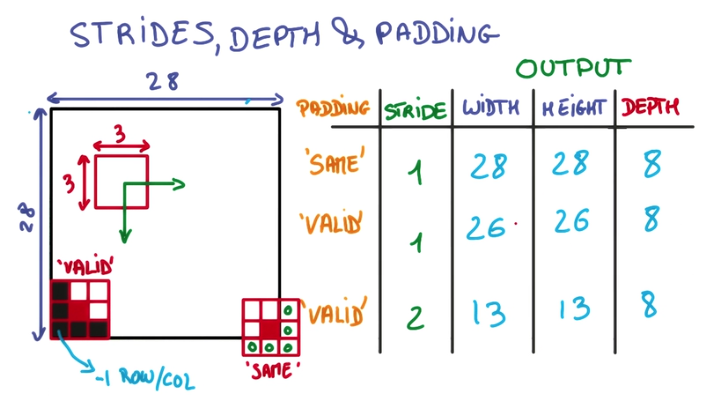
用一个3x3的网格在一个28x28的图像上做切片并移动,移动到边缘上的时候,如果不超出边缘,3x3的中心就到不了边界,因此得到的内容就会缺乏边界的一圈像素点,只能得到26x26的结果。而可以越过边界的情况下,就可以让3x3的中心到达边界的像素点,超出部分的矩阵补零就行