使用mini-batches
- batch学习: 对权重的每次迭代更新中,都需要对数据库中所有的样本过一遍,然后求解平均或者真实的梯度
- 随机或者在线stochastic (online)学习: 每次从训练集中选择(例如,随机的)一个样本{Zt, Dt}来计算梯度。这时候,梯度的估计只通过这一个样本进行估计获得。这时候的模型参数更新为:
$$
W(t+1)=W(t)-\eta\frac{\partial E^t}{\partial W}
$$
Batch学习发现的极小值是依据参数初始化在代价函数表面的某个坑上面,所以如果参数一旦初始化了,因为梯度下降都是往低的地方走,它最后一定是掉到这个坑里面。
随机学习除了学习速度比batch学习速度快之外,还可以得到更好的解,这是因为它给我们的梯度更新带来了噪声。由于噪声的存在,有时候会使参数跳到另一个坑中,从而有可能找到更深的局部极小值。更深的局部极小值意味着更小的代价函数值,也就是更拟合数据的模型。
噪声对找到更好的局部极小值很关键,但它也会阻止完全的收敛到局部极小值,它会让代价函数在极小值周围徘徊,此时,我们需要mini-batch。
mini-batch: 训练一开始,我们的参数刚初始化,离最小值还很远,这时候我们就要加快它前进的步伐,因此借助随机学习的收敛速度,我们采用一个很小的mini-batches,也就是每个batch包含的训练样本数不多。随着训练的进行,离最小值越来越近,我们就得减速了,因此我们增加mini-batches的大小,从而降低噪声。然而,每种方法的引入都会引入另外需要考虑的超参,在这里就是应该对mini-batches的大小选择怎样的增长率?这实际上和选择学习率是同样困难的。殊途同归,有效的调整学习率和有效的调整mini-batches的大小增长率效果差不多
shuffle扰乱样本学习顺序
有一个原则是,网络从意料之外的样本中学习最快。所以思想就很简单了,为了加速学习,在每次迭代的时候我们挑选一个和系统最不相似、最不和谐的样本让网络去学习。很明显,这个方法只对随机学习有效,因为batch是不管顺序的(全量)。
没有很简单的方法可以知道到底哪个输入样本携带了对系统最丰富的信息量,下面是两个简略的方法
有个的trick就是粗糙地选择来自不同类的样本,换句话来说,就是,如果在第t次迭代,我是用第i类的样本来学习的,那么在第t+1次迭代的时候,就选择除i类外的其他类的一个样本来学习。因为同一个类的训练样本很大可能携带的是相似的信息。
另一种启发式的判断到底一个训练样本携带了多少新信息的方法,就是测试当将这个样本输入到网络的时候,网络的输出值和目标输出值的误差大小。误差越大,那就表示网络还没学习到这个样本,因此它具有更多的新的信息。
随着网络的训练,每个输入样本的这个误差都会变化,所以每个样本被输入网络训练的次数也会变化。有个修改每个样本的这个概率或者次数的方法叫emphasizing scheme:
- 打乱训练集,使得邻近的样本几乎不会属于同一个类;
- 挑会使网络产生更大误差的样本输入网络学习。
注意:打乱输入样本被学习的正常频率,会改变每个样本对网络的重要程度,这可能不是那么好。如果训练集中有离群点outliers,那将带来灾难性的后果。因为离群点可以产生很大的误差,但很明显,不应该将它多次地送给网络去训练,这样会扰乱这个网络的正常学习。这个trick对一种情况非常有用,那就是可以对那些正常的但很少出现的输入模式进行性能的加速,例如在音素识别中/z/这个音素。如果这个样本是个正常的小众,那让网络多次学习它是有益的。
对输入进行标准化 Normalize
如果训练样本中每个输入变量(特征维度)的均值接近于0,那收敛一般都会更快。
考虑个极端的情况。也就是网络所有的输入都是正数。第一个隐层的神经元的参数更新值是和δx成比例的,δ是这个神经元的误差,x是输入的向量。当x所有的元素都是正数的时候,对这个神经元的参数的更新值都具有相同的符号(因为x是正数,所以更新值的符号和δ的符号一致,而δ是一个标量)。这就导致了,这些参数对一个给定的输入样本,要么全部增加(δ是正数),要么全部减小(δ是负数)。所以,如果一个参数向量到达到最优值是必须要改变方向的话,那么它就会沿着“之”形状的路径前进,这是非常低效的,所以会导致收敛非常慢。
因此,将整个训练集每个样本的输入变量的均值偏移到0处是有好处的。而且,这种启发式的方法应该在网络的每一层都使用上,即我们希望每个节点的输出的均值都接近于0
对样本缩放
有一个加速收敛的方法是对样本进行缩放,让每一个特征维度都具有相同的协方差。缩放为什么会加速学习?因为它可以平衡与输入节点连接的参数的学习率。什么意思呢?上面提到第一个隐层的神经元的参数更新值是和δx成比例的,那如果x中有些元素的值很大,而有些元素的值很小,那很明显,值大的会导致参数的更新值也很大,值小的更新值也小。这个值应该和sigmoid的选择相匹配。对下面给定的sigmoid函数,协方差取1是个不错的选择。
去除输入的相关性
考虑一种情况是,当一个输入变量总是另一个输入的两倍z2=2z1。那网络沿着线W2=v-(1/2)W1(v是个常数)的输出就都是常数。因此,在这个方向的梯度就都是0了。因此在这些线上移动对学习不会起到任何的效果。
三次变换的总结
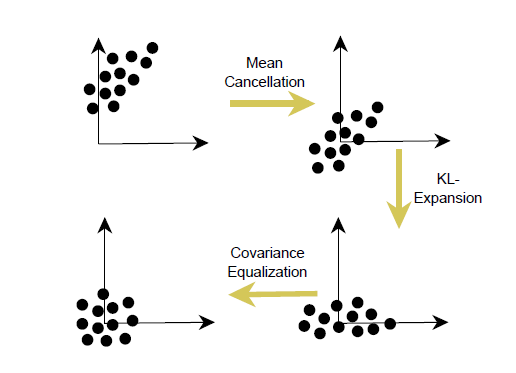
上述过程可以表达如下:1)平移输入让他们的均值为0;2)对输入解相关;3)均衡化协方差。如下图所示:
sigmod函数选择
一般取标准的逻辑函数$f(x)=\frac{1}{(1+e^{-x})}$和双曲线正切函数$f(x)=\tan h(x)$。人们往往更喜欢关于原点对称版本的Sigmoid函数(双曲线正切函数),因为上面我们提到输入应该要满足标准化,所以这个函数的输出更有可能为下一层创造均值接近于0的输入。相反,Logistic函数因为输出总是正数,因此它的均值也总是正数。
对Sigmoids函数的Tricks如下:
对称性的sigmoids函数例如双曲线正切函数往往比标准的Logistic函数收敛更快。
一个建议的激活函数是$f(x)=1.7159\tan h(\frac{2x}{3})$。因为tanh函数计算挺耗时的,所以一般可以用多项式的系数来近似。
有时候,增加一个线性项会很有用,例如f(x)=tanh(x)+ax,这样可以避免代价函数曲面flat的地方。
上述激活函数,当你使用的是标准化的输入后,这个激活函数输出的方差也会接近于1,因为sigmoid的effective gain(有效增益?)在它的有效范围内大致为1。这个特别版本的sigmoid具有以下性质:
- $f(\pm1)=\pm1$
- 最大的二次导数出现在x=1的地方;c)有效增益接近于1。
使用对称性sigmoid也有它的缺点,那就是它会使得误差表面在接近原点的地方会非常平flat。因为这个原因,所以最好可以避免将网络参数初始化为很小的值。因为sigmoids的饱和,误差表面在远离原点的时候也是flat的。在sigmoid中增加一个线性的项有时候可以避开这些flat的区域。
目标值的选择
sigmod饱和问题:网络的训练会尽自己的最大努力让网络的输出尽可能的接近于目标值,当然了,只能渐进的接近。这样,网络的参数(输出层,甚至隐层)会变得越来越大,而在这些地方,sigmoid的导数值接近于0。这些非常大的参数会增加梯度的值,然而,这些梯度接下来会乘以非常小的sigmoid导数(除非增加一个twisting扭曲项,也就是之前说的增加个线性项ax)从而导致最后的参数更新值也接近于0。最终导致参数无法更新。当输出饱和时,网络无法给出置信度的指示
方案:把目标值设置在sigmoid的有效范围内,而不是在渐进线的区域。还需要小心的是,为了保证节点不会只被限制在sigmoid的线性部分,可以把目标值设置在sigmoid的最大二阶导数的位置,这样不但可以利用非线性的优点,还可以避免sigmoid的饱和。这也是上图b中的sigmoid函数是个不错的选择的原因。它在正负1的地方具有最大的二阶导数,而正负1对应的恰好是分类问题的典型二值目标值。
参数的初始化
数初始化的原则是:参数应该随机初始化在能让sigmoid函数在线性区域激活的值。如果参数全部都很大,那sigmoid一开始就饱和了,这样就会得到一个非常小的梯度值,那参数更新就会很慢,训练也会很慢。如果参数太小了,那梯度也会很小,同样也会导致训练很慢。
参数处于sigmoid线性范围的那段区域有几个优点:
- 梯度可以足够的大,从而使得学习能正常进行
- 网络可以在学习映射的非常困难的非线性部分之前学习映射的线性部分。
如何让参数能使得sigmoid函数在线性区域激活的值:
首先,要求每个节点的输出的标准差应该接近于1,这可以通过使用之前提到的数据标准化来对训练集进行变换获得。为了可以在第一个隐层的输出同样获得标准差为1的输出,我们只需要使用上面建议的sigmoid函数,同时要求sigmoid的输入的标准差也为1。假设一个结点的输入yi是不相关的,而且方差为1,那结点的标准差就是参数的加权和:
$$
\sigma {y_i}=(\sum{j}w^2_{ij})^{\frac{1}{2}}
$$
因此,为了保证上述这个方差近似于1,参数就应该从一个均值为0,标准差为:σw=m-1/2的分布中随机采样得到(m是fan-in,也就是与这个结点连接的输入个数,也就是前一层的节点个数,如果是全连接网络的话)。
参数初始化的tricks:
假设:1)训练集已经被标准化;2)sigmoid是选择f(x)=1.7159tanh(2x/3)。
那参数就应该从一个均值为0,标准差为σw=m-1/2的分布(例如正态分布)中采样得到。
学习率的选择
大部分方法都是在参数发生震荡的时候减小学习率,而在参数相对稳定的朝着一个方向前进的时候增加学习率。这个方法的主要问题在于它对随机梯度或者在线学习是不合适的,因为参数在所有的训练过程中都是抖动的。
tricks
- 给每个参数自己的学习率;
- 学习率应该和该节点的输入个数的平方根成比例;
- 低层参数的学习率应该比高层的大。