Hessian矩阵
是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。若多元函数在临界点处一阶导数为0,此时仅仅通过一阶导数无法判断是极大值还是极小值,此时通过Hessian矩阵
若$H(m)$是正定矩阵,则M处为局部极大值。
若$H(m)$是负定矩阵,则M处为局部极小值。
若$H(m)$是不定矩阵,则M处不是极值。
泰勒级数
泰勒级数(英语:Taylor series)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。如果 在点 $x=x_0$ 具有任意阶导数,则幂级数
$$
\sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0))}{2!}(x-x_0)^2+…
$$
称为在点 $x_0$ 处的泰勒级数
拉格朗日乘子和KKT条件
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是却不知道为什么拉格朗日乘子法(Lagrange Multiplier) 和KKT条件能够起作用,为什么要这样去求取最优值呢?
下面将首先把什么是拉格朗日乘子法(Lagrange Multiplier) 和KKT条件叙述一下;然后开始分别谈谈为什么要这样求最优值。
一. 拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
通常我们需要求解的最优化问题有如下几类:
1.无约束优化问题,可以写为:
$$
min f(x);
$$
2.有等式约束的优化问题,可以写为:
$$
min f(x), \\
s.t. h_i(x) = 0;i =1, ..., n
$$
3.有不等式约束的优化问题,可以写为:
$$
min f(x), \
s.t. g_i(x) <= 0; i =1, …, n\
h_j(x) = 0; j =1, …, m
$$
对于第(1)类的优化问题,常常使用的方法就是Fermat定理,即使用求取f(x)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。
对于第(2)类的优化问题,常常使用的方法就是拉格朗日乘子法(Lagrange Multiplier) ,即把等式约束 $h_i(x)$ 用一个系数与 $f(x)$ 写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。
对于第(3)类的优化问题,常常使用的方法就是KKT条件。同样地,我们把所有的等式、不等式约束与f(x)写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为KKT条件。
拉格朗日乘子法(Lagrange Multiplier): 对于等式约束,我们可以通过一个拉格朗日系数a 把等式约束和目标函数组合成为一个式子 $L(a, x) = f(x) + a*h(x)$, 这里把a和 $h(x)$ 视为向量形式,a是横向量,h(x)为列向量。然后求取最优值,可以通过对 $L(a,x)$ 对各个参数求导取零,联立等式进行求取,这个在高等数学里面有讲,但是没有讲为什么这么做就可以,在后面,将简要介绍其思想。
KKT条件: 对于含有不等式约束的优化问题,如何求取最优值呢?常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子 $L(a,b,x)=f(x)+ag(x)+bh(x)$ ,KKT条件是说最优值必须满足以下条件:
$L(a, b, x)$ 对 $x$ 求导为零
$h(x) =0$
$a*g(x) = 0$
求取这三个等式之后就能得到候选最优值。其中第三个式子非常有趣,因为$g(x)<=0$,如果要满足这个等式,必须$a=0$或者$g(x)=0$ . 这是SVM的很多重要性质的来源,如支持向量的概念。
二. 为什么拉格朗日乘子法(Lagrange Multiplier) 和KKT条件能够得到最优值?
为什么要这么求能得到最优值?先说拉格朗日乘子法,设想我们的目标函数 $z = f(x)$, x是向量, z取不同的值,相当于可以投影在x构成的平面(曲面)上,即成为等高线,如下图,目标函数是f(x, y),这里x是标量,虚线是等高线,现在假设我们的约束 $g(x)=0$,x是向量,在x构成的平面或者曲面上是一条曲线,假设g(x)与等高线相交,交点就是同时满足等式约束条件和目标函数的可行域的值,但肯定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优值,如下图所示,即等高线和目标函数的曲线在该点的法向量必须有相同方向,所以最优值必须满足:$f(x)的梯度 = a* g(x)$ 的梯度,a是常数,表示左右两边同向。这个等式就是$L(a,x)$ 对参数求导的结果。
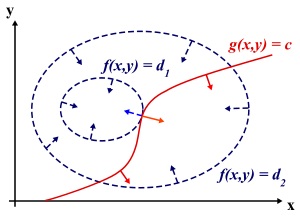
而KKT条件是满足强对偶条件的优化问题的必要条件,可以这样理解:我们要求
$$
min f(x), L(a, b, x) = f(x) + a\times g(x) + b\times h(x),a>=0,
$$
我们可以把f(x)写为:$max_{a,b} L(a,b,x)$ 为什么呢?因为 $h(x)=0, g(x)<=0$ ,现在是取 $L(a,b,x)$ 的最大值, $ag(x)\le0$ ,所以 $L(a,b,x)$ 只有在 $a\times g(x)=0$ 的情况下才能取得最大值,否则,就不满足约束条件,因此 $max_{a,b}L(a,b,x)$ 在满足约束条件的情况下就是f(x),因此我们的目标函数可以写为 $min_xmax_{a,b}L(a,b,x)$ 。如果用对偶表达式: $max_{a,b}min_xL(a,b,x)$ ,由于我们的优化是满足强对偶的(强对偶就是说对偶式子的最优值是等于原问题的最优值的),所以在取得最优值x0的条件下,它满足
$$
f(x0) = max_{a,b} min_x L(a,b,x) = min_x max_{a,b} L(a,b,x) =f(x0),
$$
我们来看看中间两个式子发生了什么事情:
$$
f(x0) = max_{a,b} min_x L(a,b,x) \
= max_{a,b} min_x f(x) + a\times g(x) + b\times h(x) \
= max_{a,b} f(x0)+a\times g(x0)+b\times h(x0) = f(x0)
$$
可以看到上述本质上是说 $min_xf(x)+a\times g(x)+b\times h(x)$ 在 $x_0$ 取得了最小值,用fermat定理,即是说对于函数 $f(x)+a\times g(x)+b\times h(x)$,求取导数要等于零,即 $f(x)的梯度+a\times g(x)的梯度+b*h(x)的梯度 = 0$
这就是kkt条件中第一个条件:$L(a, b, x)$ 对 $x$ 求导为零。
而之前说明过,$a*g(x) = 0$ ,这是kkt条件的第2个条件,当然已知的条件 $h(x)=0$ 必须被满足,所有上述说明,满足强对偶条件的优化问题的最优值都必须满足KKT条件,即上述说明的三个条件。可以把KKT条件视为是拉格朗日乘子法的泛化。
适定、超定和欠定方程的概念
矩阵的每一行代表一个方程,m行代表m个线性联立方程。 n列代表n个变量。如果m是独立方程数,根据m<n、m=n、m>n确定方程是 欠定、适定 还是 超定。
超定方程组
即方程个数大于未知量个数的方程组。
对于方程组Ra=y,R为n×m矩阵,如果R列满秩,且n>m
超定方程一般是不存在解的矛盾方程。
例如,如果给定的三点不在一条直线上, 我们将无法得到这样一条直线,使得这条直线同时经过给定这三个点。 也就是说给定的条件(限制)过于严格, 导致解不存在。在实验数据处理和曲线拟合问题中,求解超定方程组非常普遍。比较常用的方法是最小二乘法。形象的说,就是在无法完全满足给定的这些条件的情况下,求一个最接近的解。
曲线拟合的最小二乘法要解决的问题,实际上就是求以上超定方程组的最小二乘解的问题。
欠定方程组:
即方程个数小于未知量个数的方程组。
对于方程组Ra=y,R为n×m矩阵,且n<m。则方程组有无穷多组解,此时称方程组为欠定方程组。
内点法和梯度投影法是目前解欠定方程组的常用方法。
奇异矩阵
概念:奇异矩阵是线性代数的概念,就是对应的行列式等于0的方阵
判断方法:首先,看这个矩阵是不是方阵(即行数和列数相等的矩阵。若行数和列数不相等,那就谈不上奇异矩阵和非奇异矩阵)。 然后,再看此矩阵的行列式|A|是否等于0,若等于0,称矩阵A为奇异矩阵;若不等于0,称矩阵A为非奇异矩阵。 同时,由|A|≠0可知矩阵A可逆,这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵,非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵,则AX=0有无穷解,AX=b有无穷解或者无解。如果A为非奇异矩阵,则AX=0有且只有唯一零解,AX=b有唯一解
多元线性回归参数估计问题
回归参数的最小二乘估计
对于含有k个解释变量的多元线性回归模型
$$
Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+…+\beta_kX_{ki}+\mu_i
$$
设 $\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k$ 分别作为参数 $\beta_0,\beta_1,\beta_2,…\beta_k$ 的估计量,得样本回归方程为:
$$
Y_i=\bar \beta_0+\bar \beta_1X_{1i}+\bar \beta_2X_{2i}+…+\bar \beta_kX_{ki}
$$
观测值 $Y_i$ 与回归值 $\bar Y_i$ 的残差 $e_i$ 为:
$$
e_i=Y_i-\bar Y_i=Y_i-(\bar \beta_0+\bar \beta_1X_{1i}+\bar \beta_2X_{2i}+…+\bar \beta_kX_{ki})
$$
由最小二乘法可知 $\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k$ 应使全部观测值$Y_i$ 与回归值 $\bar Y_i$ 的残差 $e_i$ 的平方和最小,即使
$$
Q(\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k)=\sum e^2_i=\sum(Y-\bar Y_i)^2\
=\sum(Y_i-\bar \beta 0-\bar \beta_1X{1i}-\bar \beta_2X_{2i}-…\bar \beta_kX_{ki})
$$
取得最小值。令 $Y=(Y_i,Y_1,Y_2,..Y_n),X=(x_0,x_1,…x_n),\bar B=(\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k)$ ,上式可写为
$$
Q((\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k)=(Y-\bar BX)^T(Y-\bar BX)\
=(Y^TY-Y^TX\bar B-\bar BX^TY+\bar B^TX^TX\bar B)\
=Y^TY-2\bar B^TX^TY+\bar B^TX^TX\bar B
$$
根据多元函数的极值原理,$Q$ 分别对 $\bar \beta_0,\bar \beta_2,\bar \beta_2,..\bar \beta_k$ 求一阶偏导,并令其等于零,即
$$
\frac{\partial Q}{\partial \bar \beta _j}=0(j=0,1,2…k)
$$
即 $-X^TY+X^TX\bar B=0$ 。则为向量 $B$ 的估计量为
$$
\bar B= (X^TX)^{-1}X^TY
$$
几何概率
几何概率(geometric probability)可以用几何方法向某一可度量的区域求得的概率。向区域内投一质点,如果所投的点落在域O中任意区域g内的可能性大小与g的度量成正比,而与g的具体形状无关,则称这个随机试验为几何型随机试验或几何概率。此处的度量就是测度,一维是长度,二维是面积,三维是体积。对于几何概率,若记 $A = 质点落在区域g内$ 这一事件,则其概率定义为
$$
P(A) = \frac{L(g)}{L(\Omega)}
$$
其中 $L(g)$ 和 $L(\Omega)$ 分别为g和O的度量。这一类概率是古典概率定义的推广,它保留了等可能性,但将有限个基本事件推广到了无限。