预备知识
进一步提取LAB特征时,如何提取其中的Haar特征。中文博客
如果想知道具体的Haar特征,参考下文(英文论文原文)
二 LAB 特征
2.1 二分Haar特征
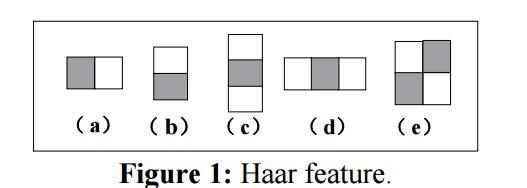
Haar特征是几个邻接矩形区域的强度差异。下图是Haar特征中矩形的一种经典出现方式,特征值即为填充矩形和非填充矩形之间的差异。更进一步说 ,矩形的布局方式是任意的。矩形区域的累积强度是可以用一种称为积分图的方式高效计算。Haar特征的计算包括增加和抽取相关矩形的累积强度。例如,对于一个2-矩形的Haar特征(图1.a和图1.b)可以如下计算:
$$
f_j(x)=(s_1)_j-(s_2)_j
$$
其中 $(s_1)_j$ 和 $(s_2)_j$ 分别代表了输入图像 $x$ 的Haar特征 $j$ 填充矩形和非填充矩形的强度和。
2.2 ABH特征
为提高二分Haar特征的区分能力,我们提出 了一种多二分Haar特征,并使用它们的共现性作为新的特征,成为ABH(Asseming Binary Haar)特征。下图演示了ABH特征的一个例子:
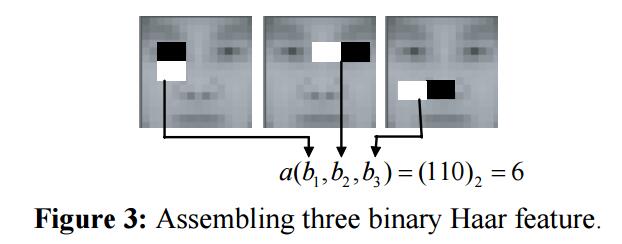
上图中ABH特征集成了三个二分Haar特征,当三个二分Haar特征值分别为1,1,0时,ABH特征为
$$
a(b_1,b_2,b_3)=(110)_2=6
$$
其中 a为三个二分Haar特征 $b_1,b_2,b_3$ 的ABH特征计算函数, $(.)_2$ 是一个从二进制转十进制的操作。特征值说明了对 $2^F$个不同结合的index,其中F是结合的二分特征数。
2.3 LAB(Locally Assembing Binary)特征
ABH特征的数目巨大。为了枚举所有的特征,需要几个自由参数,比如二分Haar特征的集合数目,每个二分Haar特征的大小,每个二分Haar特征的坐标位置。从如此巨大的特征池中学习是不可逆的。我们发现了一种对应的用于人脸检测的缩减集合,称为LAB Haar特征。
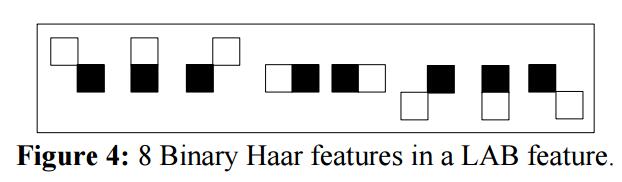
ABH特征之中,LAB特征是那些结合8个局部邻接2-矩形的二分Haar特征,它们大小相同并且共享同一个中心矩形。下图展示了一个8个二分Haar特征用以集合为一个LAB特征。
下图是一个2个LAB特征的示例
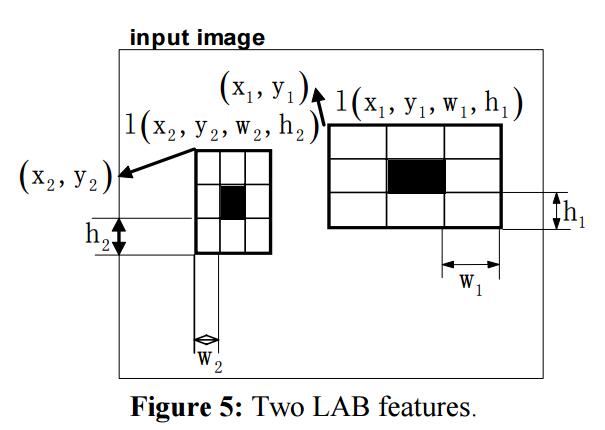
图中展示了两个不同的LAB特征,中心的黑色矩形被8个相邻的二分Haar特征共享,所有9个矩形都是相同的大小。
从公式上看,一个LAB特征可以用一个四元组表示 $l(x,y,w,h)$ ,其中 $x,y$ 分别代表了左上角的x和y轴坐标,$(w,h)$ 代表了矩形的宽和高。
LAB特征保留了所有二分Haar特征的优势,同时又很强的区分能力,大小也很小。LAB特征抓取了图像的局部强度。计算LAB特征需要计算8个2-矩形Haar特征。LAB特征值区间为 {0,…255},每个值对应了特别的局部结构。
三 使用LAB特征做人脸检测
什么是级联
级联分类器就是如下图所示的一种退化了的决策树。为什么说是退化了的决策树呢?是因为一般决策树中,判断后的两个分支都会有新的分支出现,而级联分类器中,图像被拒绝后就直接被抛弃,不会再有判断了。
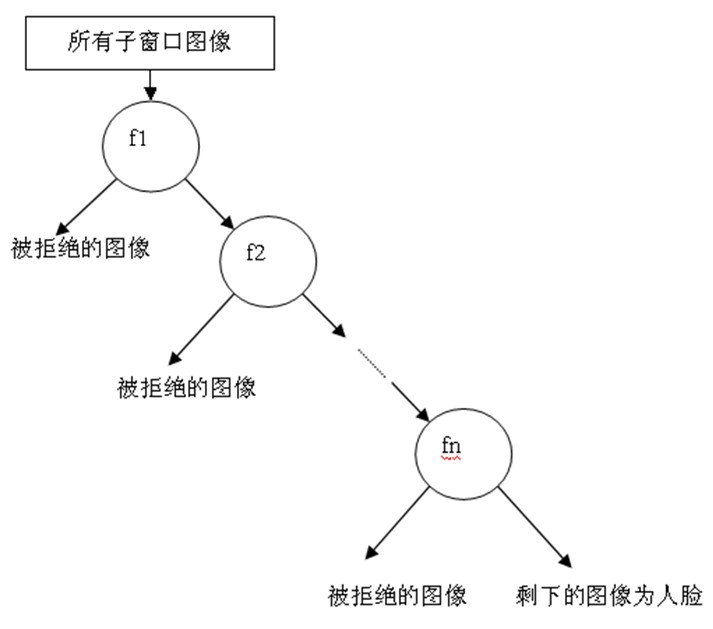
级联强分类器的策略是,将若干个强分类器由简单到复杂排列,希望经过训练使每个强分类器都有较高检测率,而误识率可以放低,比如几乎99%的人脸可以通过,但50%的非人脸也可以通过,这样如果有20个强分类器级联,那么他们的总识别率为 $0.99^20$ 约等于98%,错误接受率也仅为 $0.5^20$ 约等于0.0001%。
级联结构用于检测方法中。下图展示了人脸检测器的级联结构‘,可以分为两个很直观的部分。第一部分是一些子分类器,总称为特征中心级联。第二部分是其他的子分类器,成为窗口中心级联。
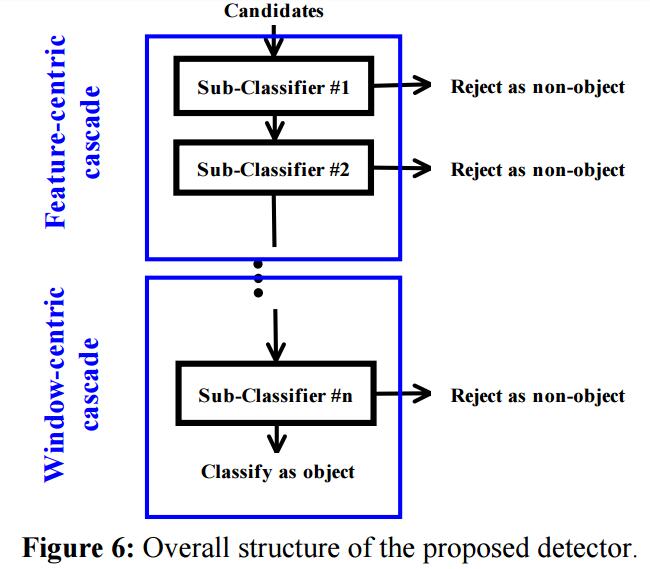
3.1 特征中心检测方法
为了搜索一张人脸,我们需要在图像中做“穷尽搜索”。这就牵扯到构造一个分类器以区分目标和非目标,却只需要在目标位置和大小上容忍有限的偏差。查找目标的方法是,扫描所有的分类器,这些分类器会在图像上搜索所有可能的位置和大小。下图展示了这一过程,所有的分类器计算了图像中所有可能的窗口,并以矩形的方式展示。
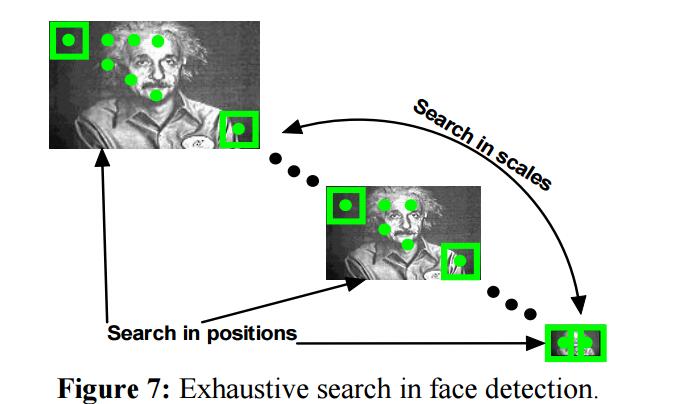
大部分级联,使用窗口中心方法。这些方法计算对每个窗口分开的计算亮度矫正和特征计算。分类器的每个可能窗口的扫描,会计算图像中每个坐标的每个特征。这说明包含在某些窗口的特征可能同时被其他分类器计算了,但是并没有被当前分类器用来分类。特征中心方法旨在使用每个窗口的更多的被计算过的特征。
如果上图不详细的话,请参考我个人绘制的示意图
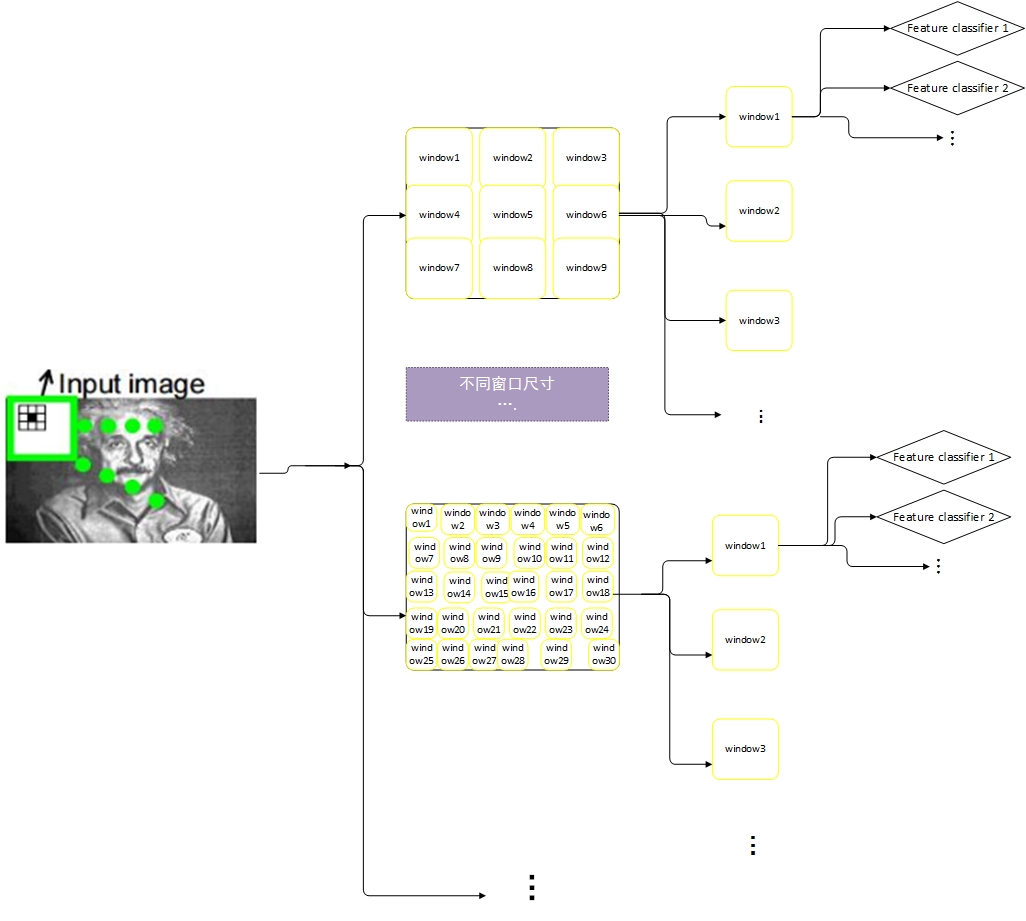
如何理解两种(窗口中心和特征中心)方法呢?下图是一个窗口中心方法的示例

窗口中心方法:对于窗口中心方法,我们假设分类器只包含了一个LAB特征。,特征为上图a中的矩形。检测时图像中每个窗口被分类。因此属于该分类器的特征同时在图像中每个位置都会被计算,这会产生一个副产品:特征值图像(上图总图b)。此示例中,对于每个窗口,只使用了一个特征来做分类,包含在窗口中的其他特征被其他临接窗口分类器计算。这存在一种计算浪费。因此,特种中心的方法被提出,用以提高计算特征的使用率。
特征中心方法:对于特征中心方法,特征值图像(下图中中间那幅,与上图中图b一样),可以通过扫描图像中所有坐标的upper特征来计算。然后特征中心的分类器会运行在特征值图像中,并不再需要特征计算操作。在学习过程中,特征中心分类器从所有属于当前窗口的所有特征中学习。实际上,所有的特征都是相同大小,因为他们都是通过在图像平移了一个特殊特征来搜集的。当然,任意大小窗口都可以用来构建特征中心分类器。但是最好是选择最有效率的一个。可以使用一种贪心所有的方法来找到最优大小。

理论上说,任意学习算法都可以用来构建窗口中心和特征中心的分类器,我们使用 RealBoost学习算法来学习线性分类函数,如下:
$$
c(x) =\sum_{i=1}^Th(l_i(x))
$$
其中 $c$ 是分类函数,$x$ 是样本窗口,$h$ 是弱分类函数,$l_i$ 是第 $i$ 个特征的特征计算函数, $T$ 是总的特征数。其中分类操作 $h$ 包含了一个特征值查阅表,一个置信度和额外查阅表。上面的Figure8和Figure9分别表示的是窗口中心和特征中心的线性分类器。Figure9中,对于所有特征中心的检测方法,分类器包含所有的窗口中的所有特征。分类函数中的特征数为 $N$ 。
3.2 特征中心级联
考虑到计算效率,我们将特征中心分类器修改为一个级联。在特征中心方法中,所有包含在窗口内的特征都被用来构建一整个的分类器。将输入图像的每个坐标点作为一个整体扫描并非明智之举。因而,我们考虑将其分解为一个级联。
两种方法的计算差异:假若分类窗口尺寸为2424,特征为33的LAB特征,因此一个窗口中会有256((24-9+1)*(24-9+1))个特征。因为对于特征中心方法和特征中心级联方法,其他过程都是相同的,因此这两种方法在各自窗口的平均分类操作代表了计算差异。对于特征中心方法,所有的256个分类操作将导致这256个特征在每个候选窗口中被操作一次。所以,每个窗口的平均分类操作数是256。但是对于特征中心级联方法,由于随着过程的推进某些窗口会被抛弃,每个窗口的平均分类操作是小于256的。
下图演示了特征中心分类器的特征和特征中心级联。图中 $l_i$ 是由RealBoost挑选出来的第 $i$ 个LAB特征, $N$ 是特征中心分类器的总特征数。圆弧箭头数代表过程的阶段数。由弧形箭头覆盖的特征是属于对应阶段地特征。
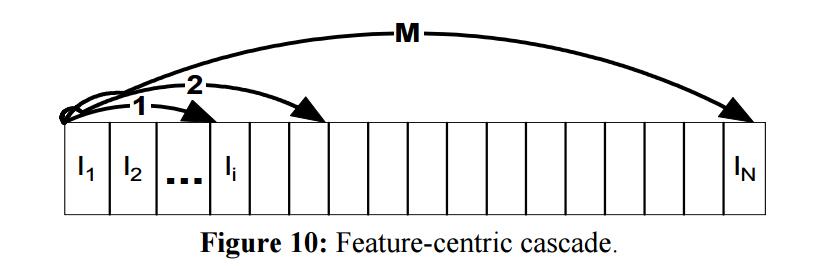
3.3 多角度人脸检测
为了构建 一个多角度人脸检测器,我们首先根据从左到右的平面旋转将所有的脸分为5个类别,然后继续将每个类别分为三个角度,每个代表了从平面30度旋转。除此之外,每个角度覆盖了[-30°,+30°]从上至下的平面旋转。下图展示了这15个不同角度。
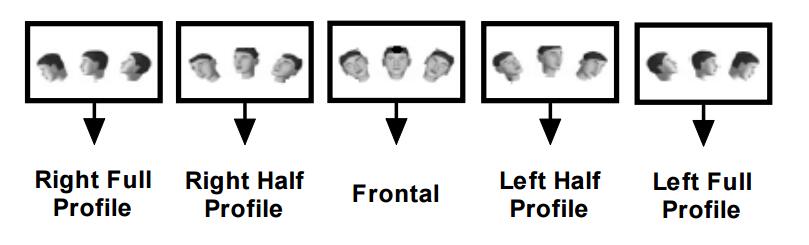
对每个角度,我们构建了一个特征中心级联和窗口中心级联。为了检测,下图展示了其过程
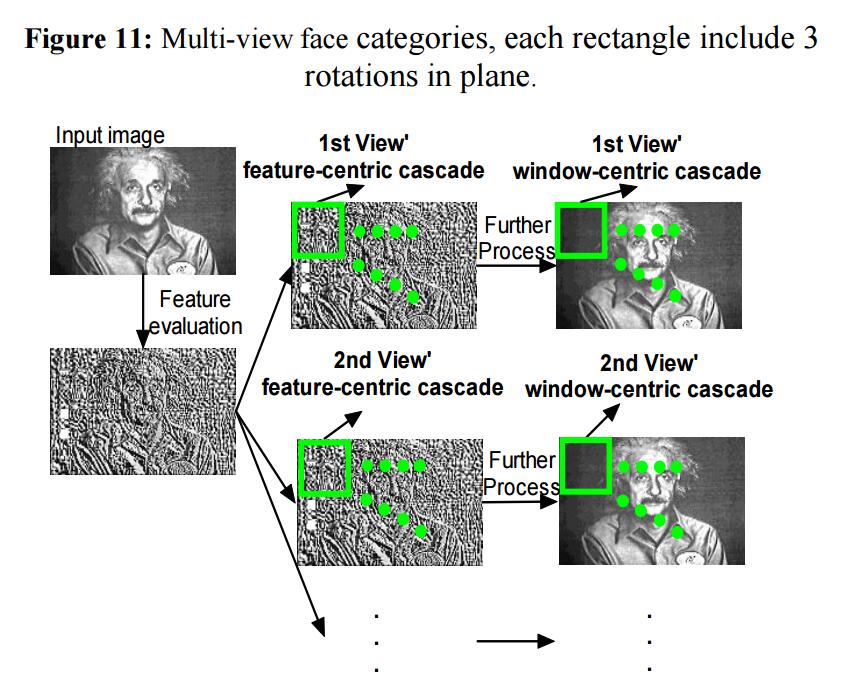
对于给定输入图像,我们首先计算特征值图像。对每个角度,特征中心级联首先基于计算特征图运行,然后窗口中心级联在原始图像上运行。注意:对于多角度人脸检测,特征值图像被所有的15个角度的特征中心级联共享。这会极大加速检测器速度。
4 实时人脸校准
4.1 CFAN简介
CFAN由4个级连的SAN网络构成,每个都是四层网络,三个隐层,用sigmoid激活,最后一层为线性激活。每一个SAN的输出图像分辨率逐渐变大,定位逐渐逼近精准
第一个全局SAN用于粗定位68个形状特征点,输入为 50x50 的低分辨率图像,即2500个输入单元,最终输出为68个形状特征点的位置,即 68x2=136个输出元素。中间层分别为1600,900,400个单元。
三个局部SAN的输入为68个特征点在高分辨率图中从周围区域提取出来的形状索引特征(SIFT)。输出仍然为逐步校正后的136个特征位置。原始输入应该是从每个形状特征点周围提取了128个SIFT特征,即共 68x128=8704个特征,太大,采用PCA的方法,分别降维到了1695、2418、2440输入元素。中间层分别为1296,784,400个单元。
4.2 训练过程
SAN的训练采用先用无监督的预训练进行分层训练,粗调参数(可采用sparse autoencoder的方法来预训练),然后用有监督的训练方法进行全局训练,精调参数。
训练样本要进行一些随机的平移、旋转、放缩,可有效防止过拟合和增加不同场合的稳定性。
全局SAN训练目标函数:
$$
F^{*}=arg\quad min_F \mid \mid S_g(x)-f_k(f_{k-1}…(f_1(x)) \mid \mid _2 ^2+\alpha \sum _{i=1}^k \mid \mid W_i\mid \mid _F^2
$$
局部SAN训练目标函数:
$$
H^*1= arg\quad min{H_1}\mid\mid \triangle S_1(x)-h_k^1(h_{k-1}^1(…h_1(\phi (S_0))))\mid \mid ^2_2+\alpha \sum_{i=1}^k\mid\mid W^1_i\mid\mid _F^2
$$
测试结果:
5 人脸对齐算法
5.1 问题
最小二乘问题中,用牛顿法求解是常用的办法,但用在求解计算机视觉的问题的时候,会遇到一些问题,比如1)、Hessian矩阵最优在局部最优的时候才是正定的,其他地方可能就不是正定的了,这就意味着求解出来的梯度方向未必是下降的方向;2)、牛顿法要求目标函数是二次可微的,但实际中未必就一定能达到要求的了;3)、Hessian矩阵会特别的大,比如人脸对其中有66个特征点,每个特征点有128维度,那么展成的向量就能达到66x128= 8448,从而Hessian矩阵就能达到8448x8448,如此大维度的逆矩阵求解,是计算量特别大的(O(p^3)次的操作和O(p^2)的存储空间)。因此避免掉Hessian矩阵的计算,Hessian不正定问题,大存储空间和计算量,寻找这样一种方法是这篇论文要解决的问题。
5.2 原理
大家都知道,梯度下降法的关键是找到梯度方向和步长,对于计算机视觉问题,牛顿法求解未必能常常达到好的下降方向和步长,如下图所示

(a)为牛顿法的下降量,收敛不能达到最理想的步长和方向。而(b)本文的SDM算法,对于不同的正面侧面等情况都能得到很好的收敛方向和步长。既然Hessian矩阵的计算那么可恶,我们就直接计算梯度下降方向和步长嘛。开始讨论之前,为方便讨论,我们需要问题形式化,假设给定一张要测试的图片(这里把图像自左向右自上而下地展成了一维的向量,具有m个像素),表示图像中的p个标记点,这篇文章里面有66个标记点,如下图黑人肖像所示。表示一个非线性特征提取函数,例如 SIFT,那么。
在训练阶段,已经知道了每张训练图片的真实的66个标记点,把这些点看做了是GroundTrue即参考点,如下图(a)所示。在测试的场景中,会用一个检测器把人脸检测出来,然后给一个初始化的平均标记点,如下图(b)所示:

那么人脸对齐问题是需要寻找一个梯度方向步长,使得下面的目标函数误差最小:
$$
f(x_0+\triangle x)=\mid\mid h (d(x_0+\triangle x))-\phi _0\mid\mid ^2_2
$$
其中 $\phi *=h(d(x))$ 是人工标定的66个标记点的SIFT特征向量,在训练阶段 $\phi _$ 和 $\triangle x$ 都是知道的。
好了,用牛顿法求解上述问题,其迭代的公式为:
$$
x_k=x_{k-1}-2H^{-1}J_h^T(\phi _{k-1}-\phi _*)
$$
其中,H和J分别表示Hessian矩阵和雅克比矩阵。它可以被进一步的拆分为下面的迭代公式:
$$
x_k=x_{k-1}+R_{k-1}\phi {k-1}+2H^{-1}J_h^T\phi*
$$
注意到,既然H和J难求,那就直接求它们的乘积,即可,于是上述的迭代公式又可以变为:
$$
x_k=x_{k-1}+R_{k-1} \phi_{k-1}+b_{k-1}
$$
其中 $R_{k-1}=-2H^{-1}J_h^T$ 和 $b_{k-1}=2H^{-1}J_h^T$ ,这样就转化为了之求解 $R_{k-1}$ 和 $b_{k-1}$ 的问题。接下来就是怎么求解这两个参数的问题了。
思路很简单,就是用训练数据告诉算法下一步该往哪里走,即用当前(及之前)的迭代误差之和最小化,该问题也是一个最优化问题。如下公式所示:
$$
arg {R_k} \quad min{b_k} \sum_{d^i}\sum_{x_k^i} \mid\mid \triangle x_*^{ki}-R_k\phi _k^i-b_k\mid \mid ^2
$$
$d_i$ 表示第i张训练图片,$x_ki$ 表示第 $i$ 张图片在第 $k$ 次迭代后的标记点的位置。实际中这样的迭代4-5次即可得到最优解,用贪心法求解。
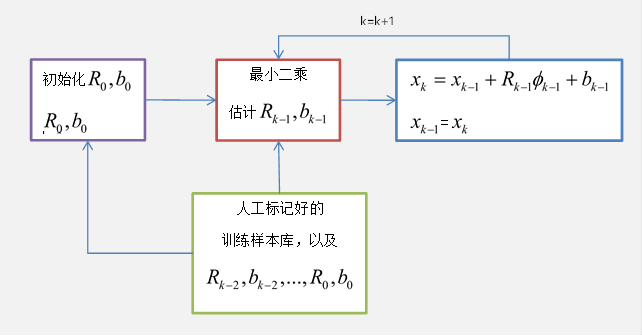
至此,根据以上描述的迭代步骤,即可不断地寻找到最优的人脸对齐拟合位置。SDM的流程图如下所示: