1 什么是循环神经网络
以NLP中的语义分析为例:输入一个词序列,经过神经网络分析,输出此词序列是正面/负面情绪。
首先,词序列会被表示为一个词向量,接着 我们查看循环神经网络和递归神经网络的处理方式。
循环结构
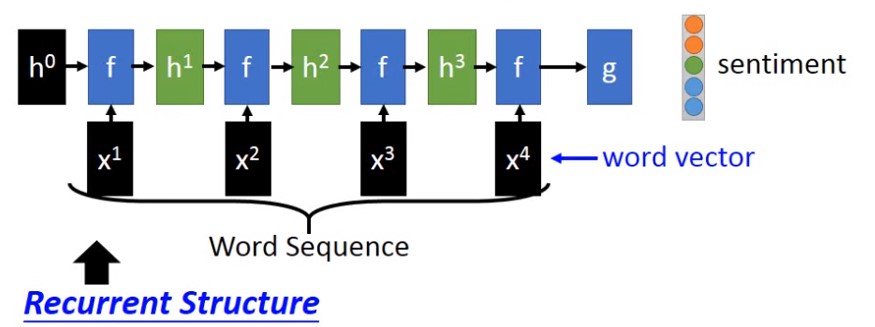
上图是一个典型的循环结构,输入为$x^1,x^2,x^3,x^4$ 这些词向量,$f$为循环神经网络的神经元,每个$f$都是一样的,最后输出的$f$经过另外一个激活函数$g$之后即可输出语音分析结果。
递归网络
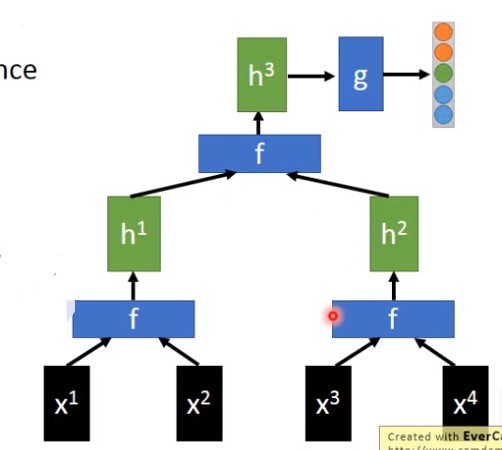
如果采取的是递归网络,我们需要先决定好输入为$x^1,x^2,x^3,x^4$ 这些词向量之间的先后依赖关系。如下图,$x^1,x^2$一起输入到函数$f$以及$x^3,x^4$一起输入到函数$f$做输出这个是需要自己事先分析并决定好的。
1.1 递归结构
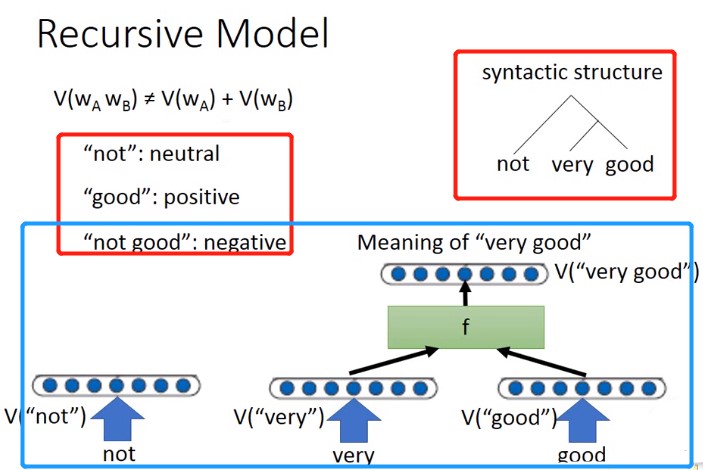
我们先了解下递归结构,假说需要分析not very good这句话的词性。会分别拆分为not,very,good,这三个单词需要按照very,good先结合之后再和not结合(这个需要我们事先决定)。对应的形式如下,至于函数$f$的形式,需要使用训练数据集学习出来:
完整的学习构建过程如下,假设我们最后需要输出5个分类,从非常负面到非常正面:
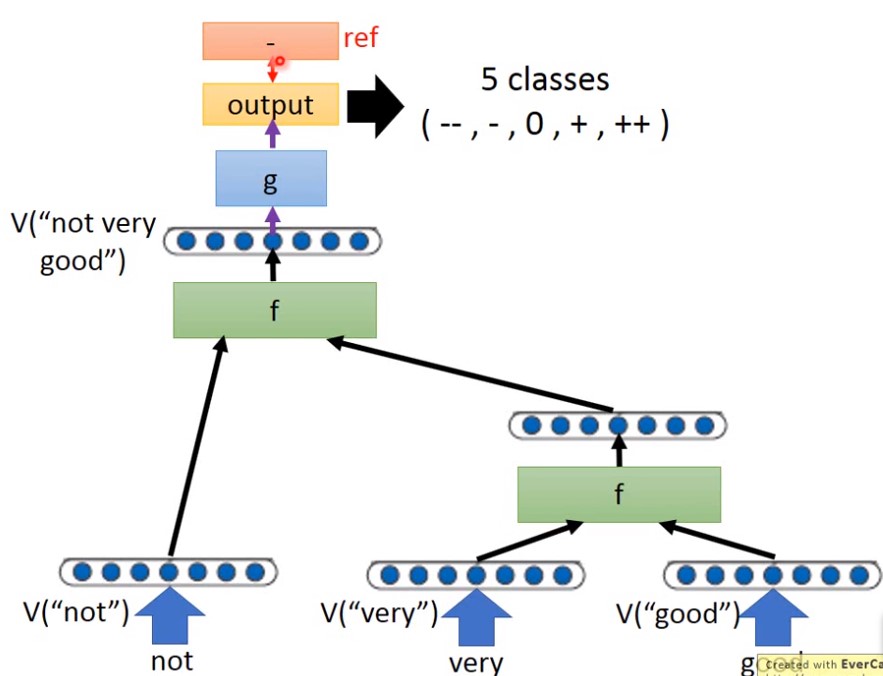
1.2 递归网络中函数f的结构
1.2.1 简单结构
最简单的结构,如下图:
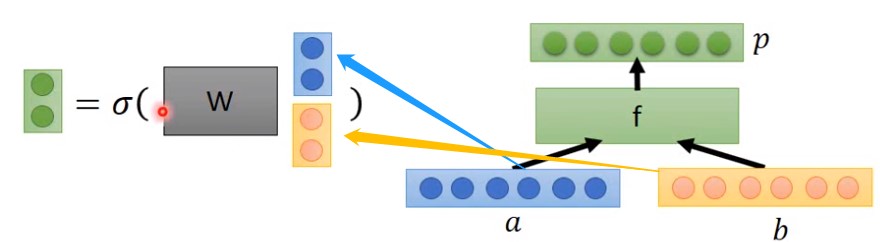
左边是计算式,右边是结构式。向量a和b串接在一起,乘以参数w(其中w是通过学习得到),得到最左边的绿色向量结果。
但是这种方式得到的结果一般并不理想,因为有些矩阵之间存在相互影响关系,比如上面演示的very和good的结合就会强化正面,very和bad结合就会强化负面。直接串接在一起只有组合和累计效果,没有相乘关系。
1.2.2 递归的Neural Tensor Network
递归的Neural Tensor Network可以产生相乘效果,如下图,除了包含上面的简单结构之外,它还做了其他组合。
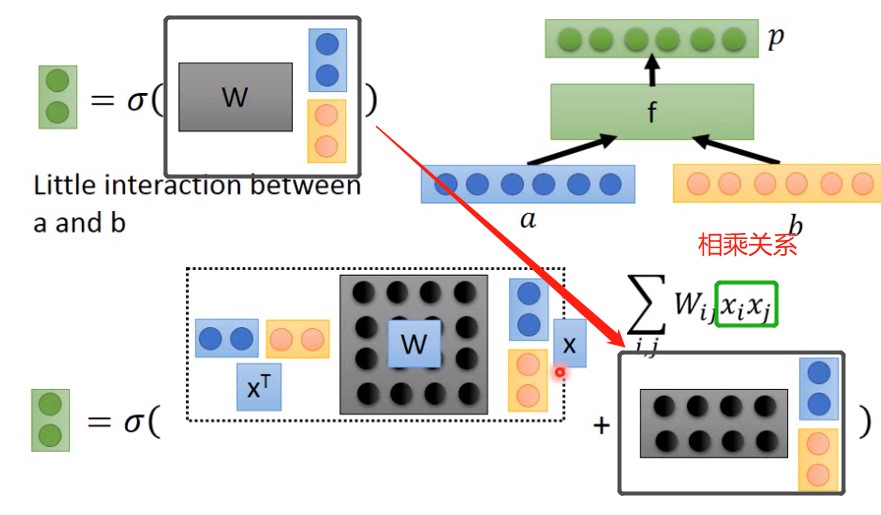
上图中,左侧黑色w左乘了x的转置并右乘了x(其中x是a和b的串接),此处他们之间运算公式为$\sum {i,j} W{i,j}x_ix_j$,注意此处出现的相乘关系。其中$x_i,x_j$分别来自蓝色和黄色矩阵。但是上图虚线框内的相乘结果是一个标量,无法直接与右侧相加的,右侧的相乘结果是$2\times 4$乘以$4\times 1$得到$2\times 1$。需要额外添加其他项,需要重复虚线框内的操作,不过将黑色w矩阵替换为一个新的矩阵,这样的一个组合就会得到一个$2\times 1$的矩阵。
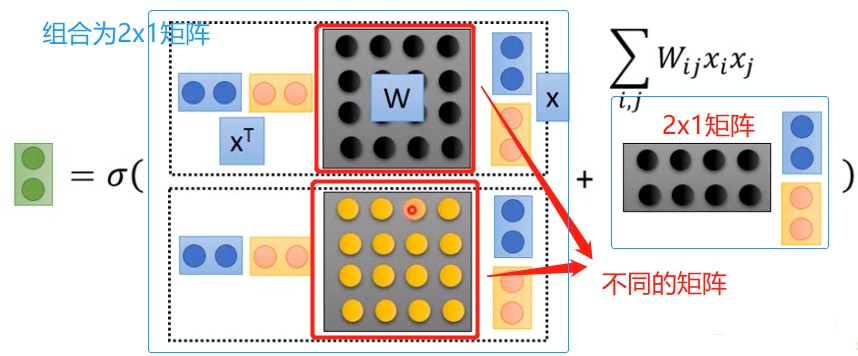
1.2 矩阵-向量(Matrix-Vector)递归网络
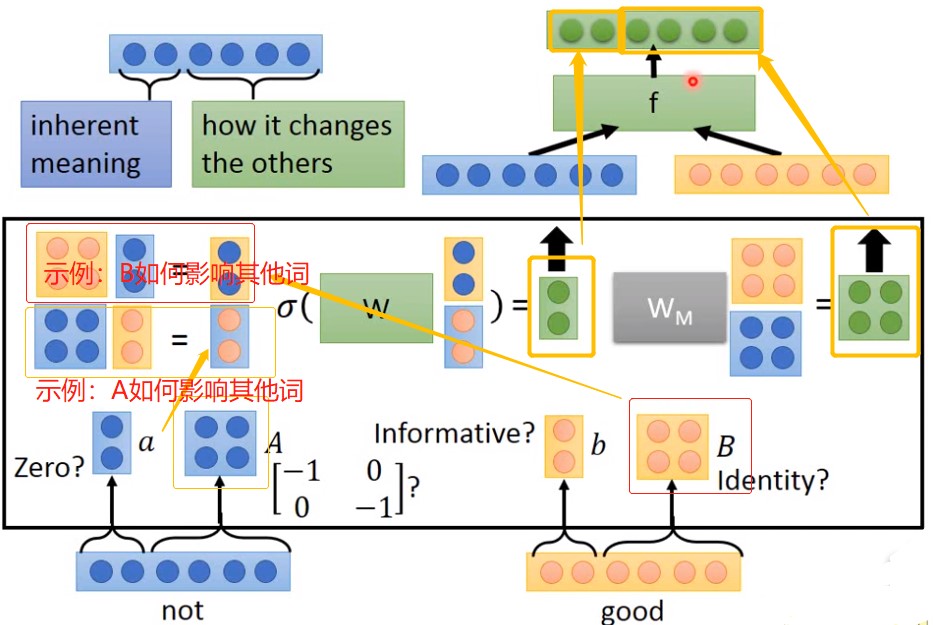
该网络以每个词都由两部分组成,即单词本身的含义和对其他词的影响,如下。
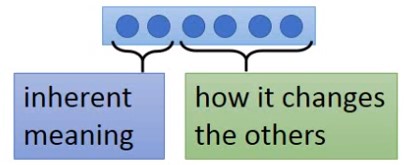
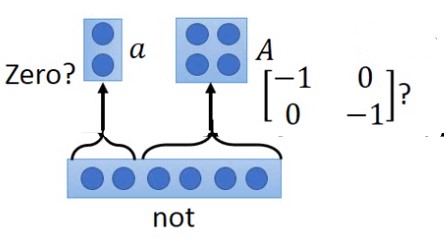
一个实例如下,比如not这个否定词的作用是对词性取反。它本身的含义可以认为是空白,对其他词的影响都是取反,所以可以分解为两部分一部分是空白向量(a),一部分是对角值为-1的向量(A)。
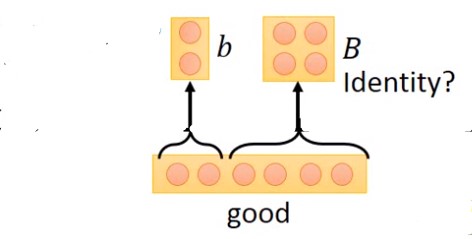
而good这个词除了表示了一种积极的信息(b)外,对其他词几乎没有影响,所以对其他词的影响部分向量可以看做一个全为1的单位向量(B),如下:
一个完整的计算过程如下,右上角展开之后的计算过程是中间的黑框内: