1 网络结构
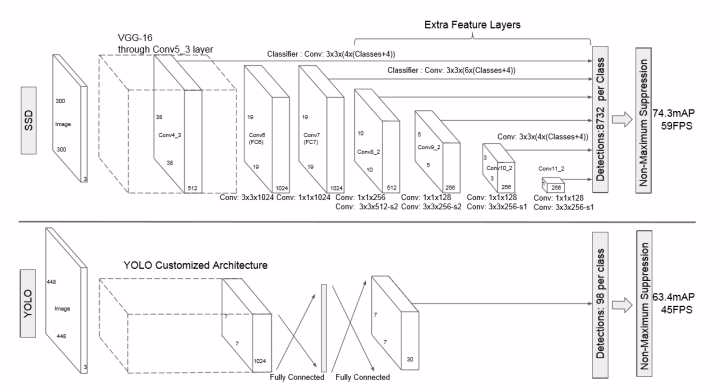
加的卷积层的 feature map 的大小变化比较大,允许能够检测出不同尺度下的物体: 在低层的feature map,感受野比较小,高层的感受野比较大,在不同的feature map进行卷积,可以达到多尺度的目的。
SSD去掉了全连接层,每一个输出只会感受到目标周围的信息,包括上下文。这样来做就增加了合理性。并且不同的feature map,预测不同宽高比的图像,这样比YOLO增加了预测更多的比例的box
横向流程图
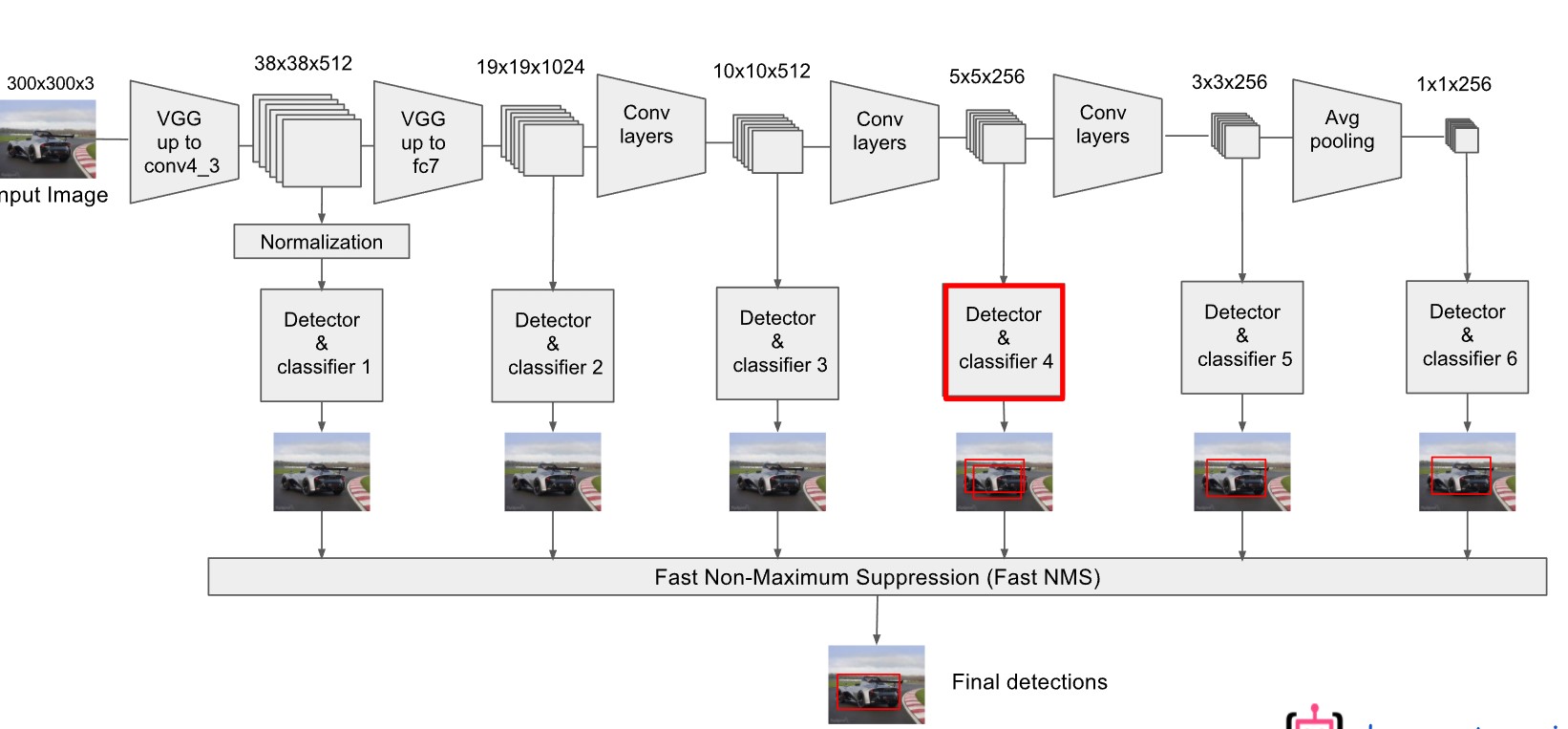
1.1 网络结构(代码)
basenet 以VGG-19为例。
代码如下:
第一段是 VGG-19
1 | # Input image format |
第二段为SSD使用的6个额外的特征层(接上面的)
1 | fc6 = Conv2D(1024, (3, 3), dilation_rate=(6, 6), activation='relu', padding='same', kernel_initializer='he_normal', name='fc6')(pool5) |
对conv4_3的输出做正则化处理
1 | # Feed conv4_3 into the L2 normalization layer |
接下来的步骤是基于basenet的结果做多层输出。 包含以下几个特征层
- conv4_3_norm
- fc7
- conv6_2
- conv7_2
- conv8_2
- conv9_2
2 分类和回归
顺着代码继续走。接下来是解析 上图中 Detector & classifier 这部分的代码。
需要了解的是上面的Detector & classifier 这部分操作其实由三部分组成。以Detector & classifier 4为例,如下图:
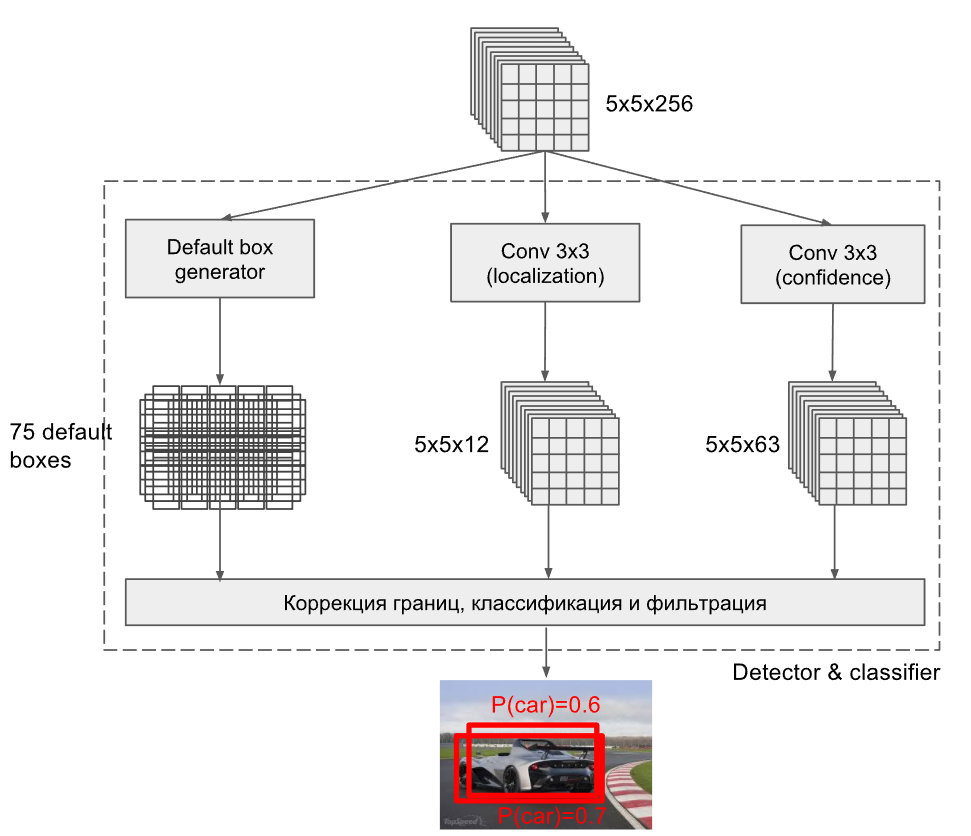
做了 三个操作:
- 生成 anchor box
- 做卷积->定位(localization)
- 做卷积->分类(confidence)
注意上图默认是每个feature map上每个点生成3个 priorbox,所以一共生成了75个。
2.1 卷积->分类
直接看源码如下:
1 | # we predict 'n_classes' confidence values for each box,hence the confidence predictors have depth 'n_boxes*n_classes' |
需要注意的是卷积核数目是跟分类数目相关。假设某一层feature map的size是 $m\times n$,通道数是 $p$。例如上面展示的 Detector & classifier4就是 $m=5,n=5,p=256$。做分类时所有的卷积核都是3x3xp(上面的代码没有体现出p),而输出通道数是 $n_{boxes}\times n_{classes}$ (代码中的n_boxes和n_classes)
n_boxes代表的是default box(从feature map上自动生成的方框)。不同feautre map层的n_boxes不同,一般是4或6.
2.2 卷积->回归(其实还是卷积)
从feature map中回归得到 每个预测框的 $x(中心点x坐标),y(中心点y坐标),w(预测框的宽度),h(预测框的高度)$ 。同样使用 $3\times 3$的卷积核(理论上应该是 $3\times3\times p$)。
1 | ## predict 4 boxes for coordinates for each box,hence the localization predictors have depth 'n_boxes*4' |
与上面的一致,只不过输出通道数变为 $n_{boxes}\times 4$,最后乘以4,代表的是对每个default box(从feature map上自动生成的方框)的位置信息。
2.4 生成prior box(default box)
注意,此时已经有两个地方生成box了。一个来自2.2步的卷积,一个是这一步由新的keras层生成。这一步生成的box是模板形式的,而且最后一个维度是8(2.2步生成的是4)是4个location维度+4个偏置(回归所需的参数)。
论文中并没有提到prior box是基于什么生成的,看图的话会以为是直接从feature map中生成,从代码来看,prior box是从位置回归的feature map中生成,这一点与第二节开始的那个图(生成75个box)不太一致,此处暂时按照代码的思路走。代码如下:
1 | ## Generate the anchor box(called "priors" in the original caffe/c++ implemention ) |
注意 priorbox的输入是 box_loc。上面的 AnchorBoxes是重写了一个Keras的网络层。
2.5 如何生成prior box
2.5.1 理论
prior box是按照不同的 scale 和 ratio 生成,m(默认是6,但是有的层不一定,比如conv4_3层的是3(实际上因为对于ratio=1的会多生成一个,所以是4个))个 default boxes,这种结构有点类似于 Faster R-CNN 中的 Anchor。(此处m=6所以:$5\times 5\times 6$ = 150 boxes)。
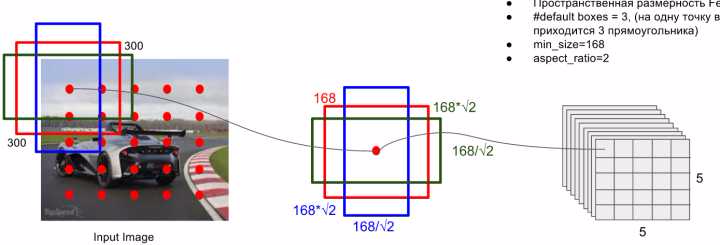
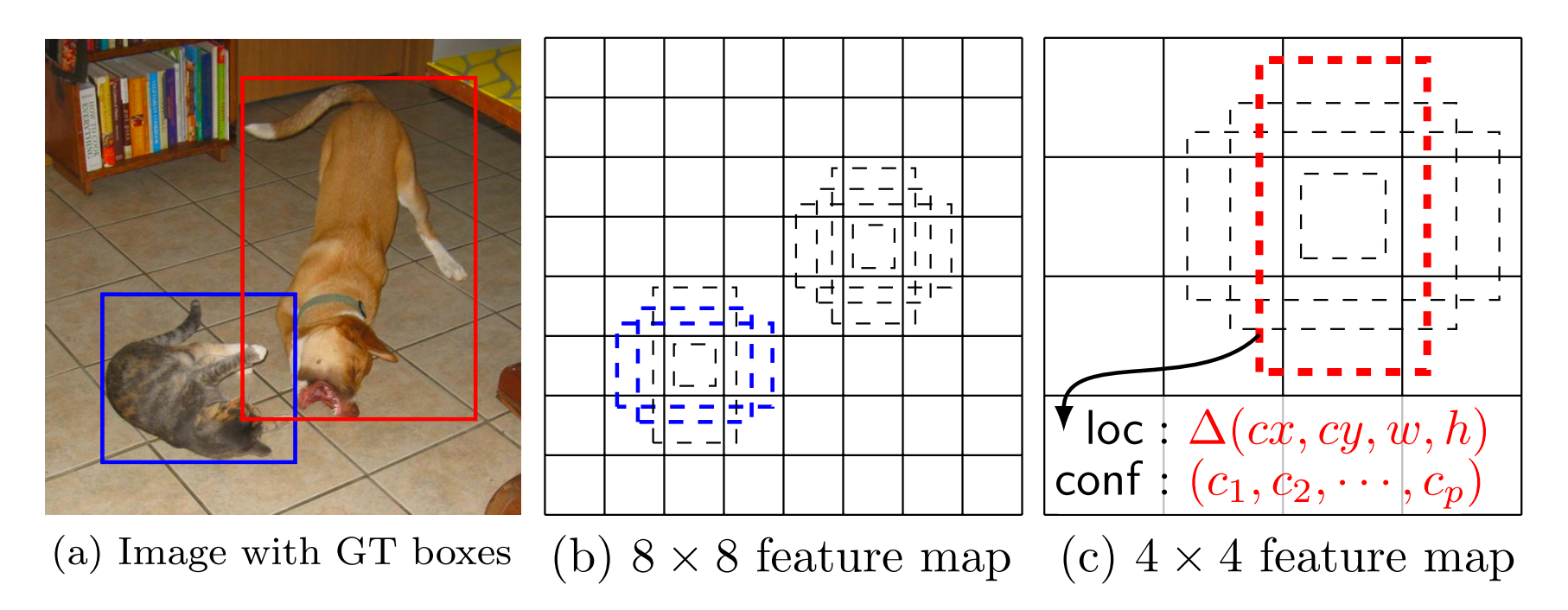
上图中从左到右依次是:原图,以特征图中一个像素点为中心生成的3个priorbox(不同宽和高),特征图(256x5x5)。
scale: 假定使用N个不同层的feature map 来做预测。最底层的 feature map 的 scale 值为 $s_{min}=0.2$,最高层的为$s_{max} = 0.9$ ,其他层通过下面公式计算得到 $s_k = s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1), k\in [1,N]$ (低层检测小目标,高层检测大目标)。当前$300\times3\times3$网络一共使用了6(N=6)个feature map,即网络结构图中的detector1..detector6。比如第一层detector1的$s_k=0.2$,第二层的detector2的$s_k=0.2+\frac{0.9-0.2}{6-1}(2-1)=0.34$,…第五层detector5的$s_k=0.2+\frac{0.9-0.2}{6-1}(5-1)=0.76$
ratio: 使用不同的 ratio值 $a_r\in \lbrace 1,2,\frac{1}{2},3,\frac{1}{3}\rbrace$ 计算 default box 的宽度和高度: $w_K^{a} = s_k \sqrt{a_r} , h_k^{a} =s_k/\sqrt{a_r}$ 。另外对于 ratio = 1 的情况,额外再指定 scale 为 $s_k{`}=\sqrt{s_ks_{k+1}}$ 也就是总共有 6 中不同的 default box。比如示意图中的为detector4,其$s_k=0.62$,依据公式 $w_K^{a} = s_k \sqrt{a_r}$ 按照 $\lbrace 1,2,\frac{1}{2},3,\frac{1}{3}\rbrace$ 顺序可以有 $w_k^a$ : $[0.62\times300,0.62\times1.414\times300,0.62\times0.707\times300,0.62\times1.732\times300,0.62\times0.577\times300]$ 。与图中的168不一致
default box中心:上每个 default box的中心位置设置成 $(\frac{i+0.5}{\vert f_k \vert},\frac{j+0.5}{\vert f_k\vert})$ ,其中 $\vert f_k \vert$ 表示第k个特征图的大小 $i,j\in [0,\vert f_k\vert]$ 。
注意:每一层的scale参数是
注意这些参数都是相对于原图的参数,不是最终值
2.5.2 代码解析
我把ssd_box_encode_decode_utils.py代码里面关于如何生成prior box的部分精简部分提取出来如下,注意生成prior box的代码是一个类AnchorBoxes:
先看构造方法里面的参数
1 | def __init__(self, |
依次解析参数。
- img_height:原始输入图像的尺寸
- img_width:
- this_scale:当前feature map的scale
- next_scale:下一个feature map的scale。至于用处,下面的代码会说明
- aspect_ratios=[0.5, 1.0, 2.0] :当前feature map即将生成的每个prior box的ratios,它的长度即当前feature map上每个特征点会生成的prior box数目。
- two_boxes_for_ar1=True:对于ratios=1的特征层是否多生成一个 prior box
- limit_boxes=True :是否限制boxes的数目
- variances=[1.0, 1.0, 1.0, 1.0]: 这个参数是用来和 two_boxes_for_ar1配合使用,用来处理如何多生成一个prior box的
- coords=’centroids’:坐标体系,是$(x,y,w,h)$还是$(x_{min},y_{min},x_{max},y_{max})$
- normalize_coords=False:是否归一化
接下来看call(self,x)函数,该函数里面写明了如何处理数据,如何生成priorbox。
2.5.3 获取每个cell的尺寸
cell代表的是将原图切割成 feature_map_width * feature_map_height个小矩形格。代码keras_layer_AnchorBoxes的call方法中演示了如何根据每个特征层生成priorbox。代码做了两个操作
获取每个cell的宽和高
获取每个cell的 起始坐标(左上角的x,y)
为了演示如何处理,我单独测试这个代码。假设测试的特征层为上图的 $5\times5\times5\times256$ ,让所有的值为1.
1 | input = np.ones([16,5,5,512],dtype=np.int16) |
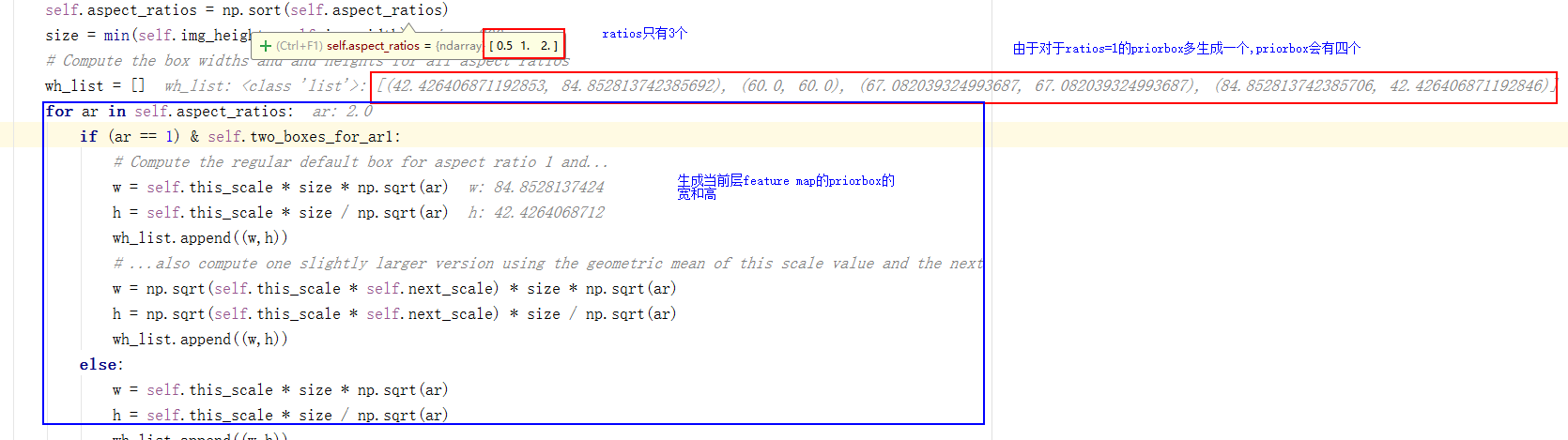
当前层feature map的ratios = [0.5,1,2],根据公式$w_K^{a} = s_k \sqrt{a_r} , h_k^{a} =s_k/\sqrt{a_r}$。计算 priorbox的宽和高,注意中间都会乘以size(原图尺寸参考)。
以下图的168为例,

然后将原图划分cell,依据是当前feature map大小。比如下面的代码中,feature map大小是 $5\times 5$,原图大小是 $300\times300$,那么每个cell尺寸是 $\frac{300}{5}\times \frac{300}{5}=60\times60$
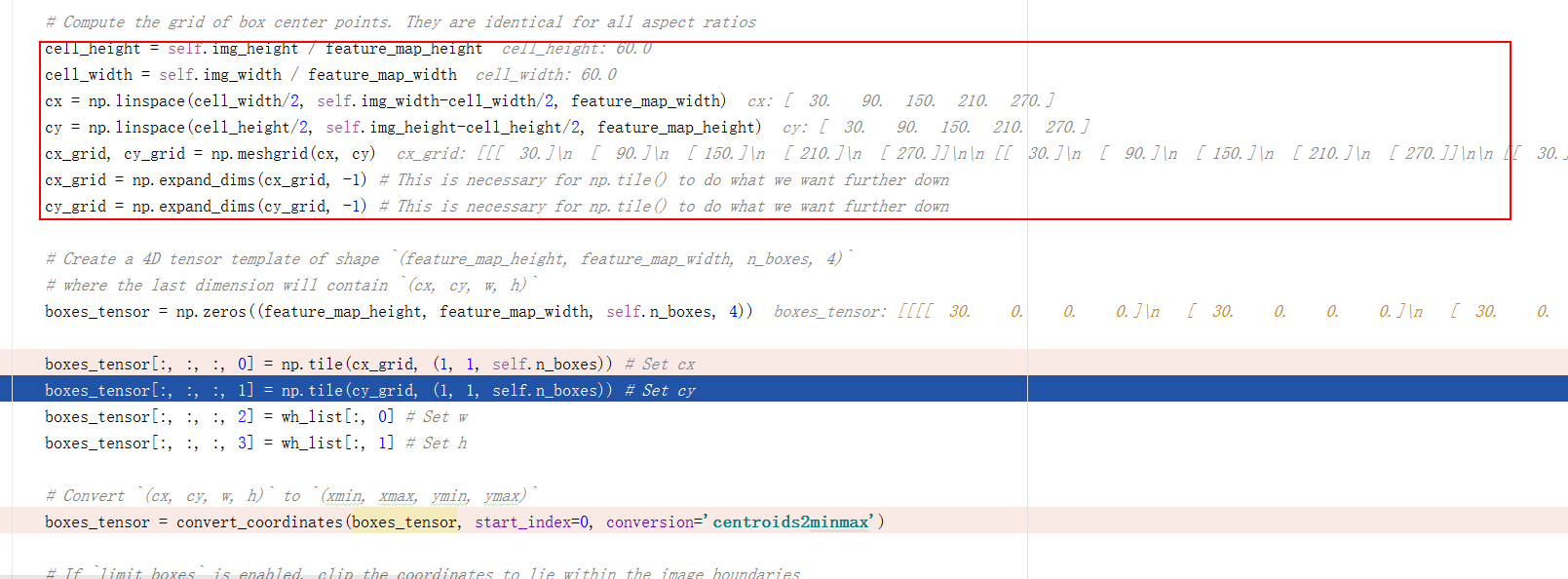
上面这一步做的其实是下图
不同的feature map的cell宽和高不同。依据feature map将原图划分为等额的cell,**红框部分是获取每个cell在原图里的起始坐标点(x,y)**。
注意boxes是如何产生的 boxes_tensor = np.zeros((feature_map_height, feature_map_width, self.n_boxes, 4)) 创建了一个 size= [feature_map_height,feature_map_width,n_boxes,4] 的四维矩阵。代表的是每个feature map的每个特征点有n_boxes个priorbox,而每个priorbox有x,y,w,h四个参数来定义一个priorbox。
接下来是把priorbox超出原图边界的修正下。
然后再创建一个variances_tensor,它和上面的boxes_tensor维度一样,只不过它的值都为0加上variance(尺寸和n_boxes一样).然后将variances_tensor和boxes_tensor做连接(concatenate)操作。所以生成的priorbox 会变成 size= [feature_map_height,feature_map_width,n_boxes,8] (论文里面不会说得这么具体)
下图可以看出,原图中两个动物分别在不同层次的detector & classifier 被检测出来。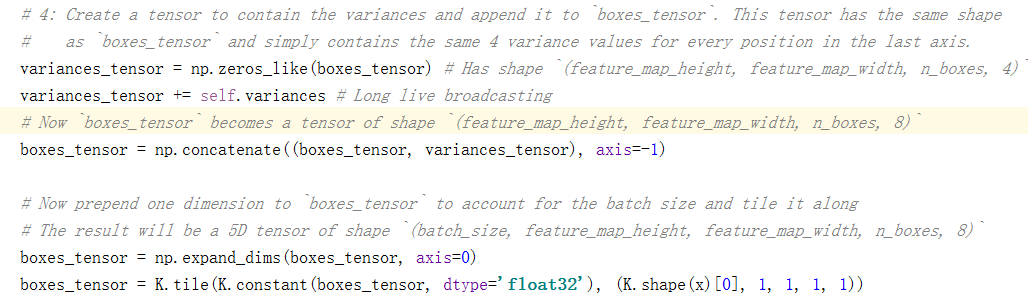
2.6 Reshape
接下来变换特征矩阵便于做统一处理。
1 | # reshape the predict class predictoins,yield 3D tensor of shape '(batch,height*width*n_boxes,n_classes)' |
如何理解这一步的操作?
比如feature map为 $5\times 5\times 256$ (对应的是conv8_2_mbox_conf)这一层,如何运算到当前步骤(不考虑batch)。
- 【分类】做$3\times3$卷积运算,输入通道数是 256,卷积数目是 n_boxes_conv6_2*n_classes(注意不是n_boxes_conv8_2n_classes)【见2.1节,没有改变feature map大小】,那么输出矩阵是[n_boxes_conv6_2n_classes,5,5] 。n_boxes_conf6_2 = 4,假设是20个分类(要加一个背景分类),那么产生新的feature map尺寸为[21x4,5,5]。对应的会生成一共 $21\times4\times5\times5=2100$个priorbox
- 【回归】做$3\times3$卷积运算,输入通道数是 256,卷积数目是 n_boxes_conv6_2*4(注意乘以的是4,不是分类数)【见2.2节,没有改变feature map大小】,那么输出矩阵是[n_boxes_conv6_2*4,5,5] 。n_boxes_conf6_2 = 4),那么产生新的feature map尺寸为[4x4,5,5]。对应的会生成一共 $4\times4\times5\times5=400$个priorbox
- 【生成priorbox】,从上一步【回归】的矩阵输出 $4\times4\times5\times5$,feature map大小是 $5\times5$,当前层每个特征点生成4个priorbox,每个priorbox有
x,y,w,h四个参数。这一步才是真的填补priorbox的四个参数,并且添加了每个参数的偏置variance,变成8.(即$8\times4\times5\times5$) - 【reshape】
- 对【分类】步骤的结果reshape:[n_boxes_conv6_2*n_classes,5,5](即[21x4,5,5])–>[-1,n_classes](即[100,21])
- 对【回归】步骤的结果reshape: [n_boxes_conv6_2*4,5,5] (即[4x4,5,5])–>[-1,4](即[100,4])
- 对【priorbox】步骤的结果reshape:[n_boxes_conv6_2*8,5,5](即[4x8,5,5])–>[-1,8](即[100,8])
2.8 连接concatenate
连接所有的分类,回归,priorbox
1 | ## Concatenate the prediction from different layers |
所以从代码上来看,所有的分类走一条线,回归走一条线,生成priorbox走一条线(中间是从回归那边过来)。一条线的意思是,从basenet开始到最后添加的所有的feature map层处理这一段流程。从论文来看回归即priorbox,但是代码上来看是分开的
回归loc和priorbox所生成的结果是相互独立的,而分类的结果之间是相互影响的(每个分类都有个单独的结果),需要做一个softmax实现多分类。
1 | mbox_conf_softmax = Activation('softmax',name='mbox_conf_softmax')(mbox_conf) |
最后做个汇总,把分类、回归、priorbox连接起来。
1 | # concatenate the class and box predictions and the anchor box |
注意是在最后一个维度连接,最后的维度是 n_classes+4+8
3 数据生成generator
从源代码来看,generator相当复杂。我们可以只关注ssd_batch_generator.py中的generator方法,可以看到里面做了大量的数据增强。我们顺序来看
数据混排

等值变换(增强对比度)

明暗度变换

水平翻转

等等。。
4 如何生成训练样本(正/负Box)
AnchorBox是FasterRCNN的叫法,SSD的是PriorBox。下面的代码是ssd_box_encode_decode_utils的encode_y方法。通过这个方法可以知道代码里面是如何生成正/负样本的。
方法传入的是一张图片的所有真实bbox,即[(分类1,xmin,ymin,xmax,ymax),(分类2,xmin,ymin,xmax,ymax),…]。注意,从下面这段代码可以看出,没有直接使用真实的标注bbox,而是使用与真实bbox重叠超过一定比率的预设priorbox作为正样本,小于一定比率的为负样本
大概过程如下:
- 先收集整个网络的PriorBox。包含了根据SSD所有特征层生成的PriorBox。作为全部正样本候选
- 拷贝一份正样本,作为负样本的候选。
- 计算每个正样本与全部真实标记框的IOU
- 1 如果所有的PriorBox与真实标记得IOU都没有高于阈值的,则将有最高IOU的PriorBox作为正样本。同时从负样本中剔除该PriorBox
- 2 IOU高于阈值的PriorBox会作为正样本保留,同时将对应的priorbox从负样本中剔除

4.1 如何在矩阵中做变换的
回顾2.8节,SSD网络的最后输出是 **[box_feature,n_classes+4+8]**。
我们考虑下矩阵是如何变换的,下面的列表是依次说明每一列所代表的意义。
| index | 标记 | 意义 |
|---|---|---|
| [0,..] | box_feature | 所有的box |
| 1 | if_class | 背景分类的概率 |
| 2 | if_class | 分类1的概率 |
| 3 | if_class | 分类2的概率 |
| 4 | if_class | 分类3的概率 |
| … | … | 分类n的概率 |
| n+1 | xmin | SSD网络预测的可能的box的坐标xmin) |
| n+2 | xmin | SSD网络预测的可能的box的坐标ymin) |
| n+3 | xmin | SSD网络预测的可能的box的坐标xmax |
| n+4 | xmin | SSD网络预测的可能的box的坐标ymax |
| n+5 | box_xmin | 生成的PriorBox的坐标xmin |
| n+6 | box_ymin | 生成的PriorBox的坐标ymin |
| n+7 | box_xmax | 生成的PriorBox的坐标xmax |
| n+8 | box_ymax | 生成的PriorBox的坐标ymax |
| n+9 | box_x_var | 将网络预测的xmin调整到真实xmin所需的参数 |
| n+10 | box_y_var | 将网络预测的ymin调整到真实ymin所需的参数 |
| n+11 | box_wth_var | 将网络预测的box的宽度调整到真实box宽度所需的参数 |
| n+12 | box_hgt_var | 将网络预测的box的高度调整到真实box高度所需的参数 |
注意:
SSD网络预测的可能的box的坐标: 这个结果你可以当做普通卷积的一个输出结果,跟PriorBox无关生成的PriorBox的坐标:指的是在feature map参照下生成的各个priorbox坐标。这个是模板形式,任意图片进来都是相同的值。它的作用是产生正/负样本,真实坐标是没有直接参与训练的,priorbox坐标与真实坐标iou大于阈值的为正,小于另外一个阈值的为负。
添加测试代码:
1 | aspect_ratios_per_layer = [[0.5, 1.0, 2.0], |
我们先分析生成生成Box的数量问题。通过调试上面的测试代码,可以看到
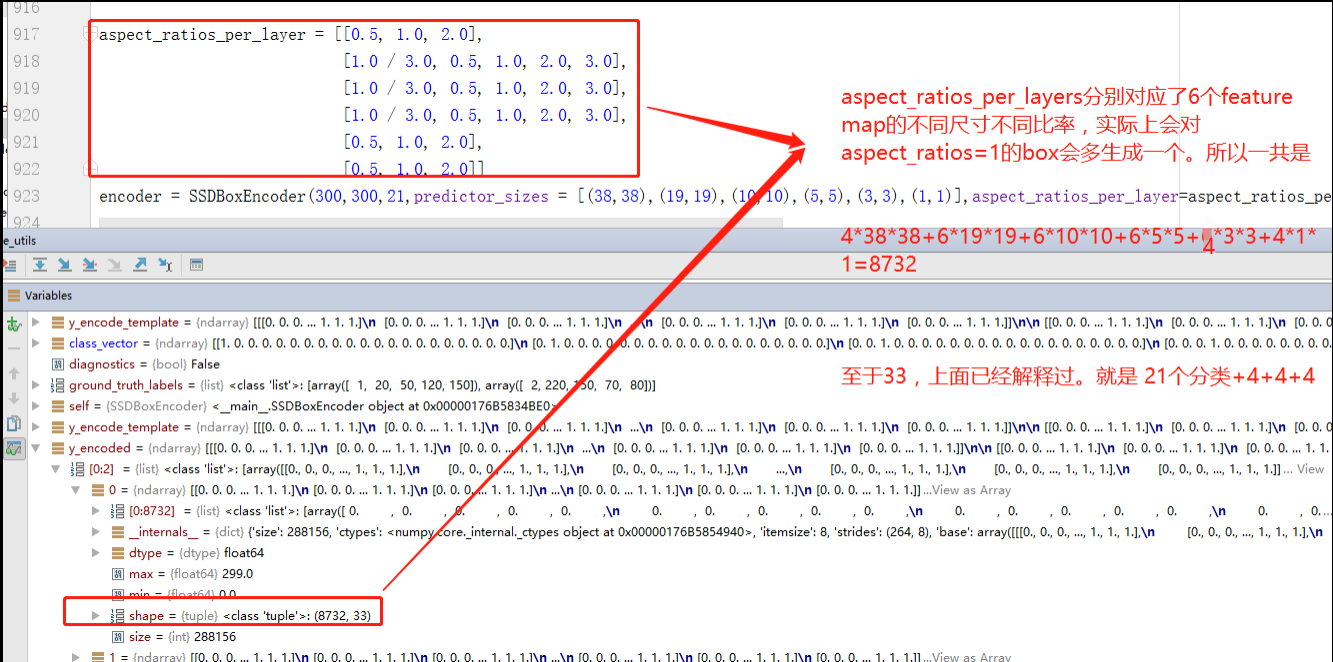
下面再对shape的后一个size 33做出解释。
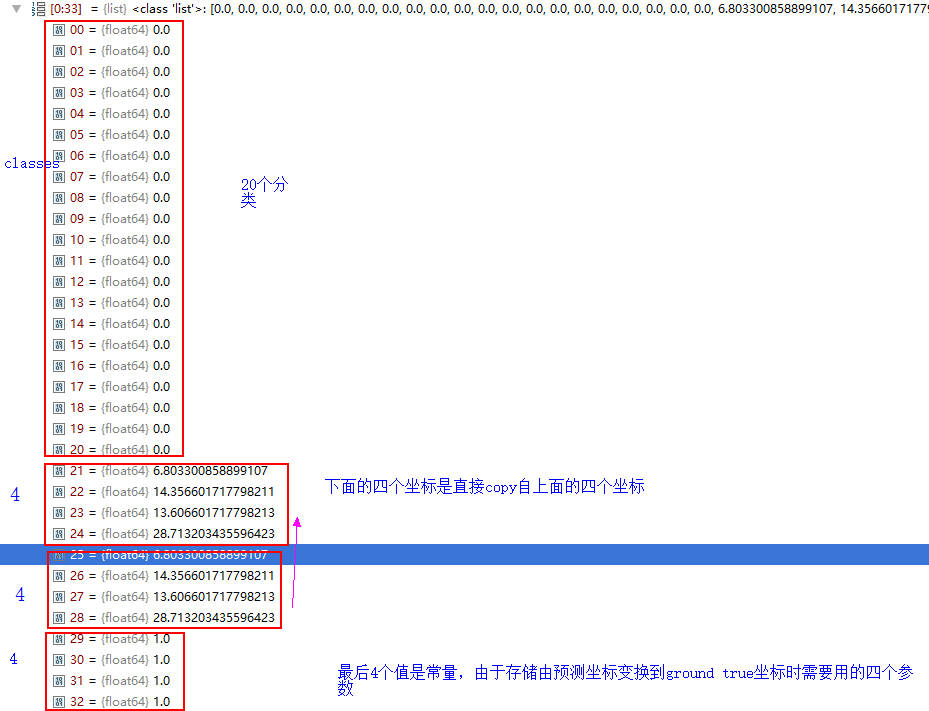
4 损失函数
损失函数的代码在keras_ssd_loss.py这个类中。
4.1 理论
目标函数,和常见的 Object Detection 的方法目标函数相同,分为两部分:计算相应的 default box 与目标类别的 score(置信度)以及相应的回归结果(位置回归)。置信度是采用 Softmax Loss(Faster R-CNN是log loss),位置回归则是采用 Smooth L1 loss (与Faster R-CNN一样采用 offset_PTDF靠近 offset_GTDF的策略)。
$$
L(x,c,l,g) = \frac{1}{n}(L_{cof}(x,c)+\alpha L_{loc}(x,l,g))
$$
其中N代表正样本数目。回归损失函数如下:
$$
L_{loc}(x,l,g) =\sum ^N_{i\in Pos}\sum_{m\in \lbrace cx,cy,w,h\rbrace}x_{i,j}^k smooth_{L_1}(l_i^m-\hat g_j^m) \
\hat g_j^{cx}= \frac{(g_j^{cx}-d_i^{cx})}{d_i^w} \
\hat g_j^{cy}= \frac{(g_j^{cy}-d_i^{cy})}{d_i^h} \
\hat g_j^w= \frac{(g_j^w-d_i^w)}{d_i^w} \
\hat g_j^h= \frac{(g_j^h-d_i^h)}{d_i^h}
$$
分类损失函数如下:
$$
L_{conf}(x,c) = \sum {i\in Pos}^Nx{ij}^plog(\hat c_i^p)-\sum_{i\in Neg}log(\hat c_i^0) \quad\quad 其中 \hat c_i^p = \frac{exp(c_i^p)}{\sum_pexp(c_i^p)}
$$
4.2 代码中的详细计算
# 1: Compute the losses for class and box predictions for every box
classification_loss = tf.to_float(self.log_loss(y_true[:,:,:-12], y_pred[:,:,:-12])) # Output shape: (batch_size, n_boxes)
localization_loss = tf.to_float(self.smooth_L1_loss(y_true[:,:,-12:-8], y_pred[:,:,-12:-8])) # Output shape: (batch_size, n_boxes)
```
可以看到计算loss的时候是分别取出对应部分值的。注意**2.8节**最后的维度是 **n_classes+4+8**,上面计算classification_loss的时候是取得**n_classes**部分,localization_loss取的是`4`(回归得到的priorbox的四个参数)。**此处最后的`8`没有使用,这个`8`是生成的priorbox的4个参数和4个参数的偏置,只有在inference的时候需要使用**。
**生成模板**
`generate_encode_template`主要做了一下操作:
1. 给所有特征层生成box。包括宽、高、坐标、尺寸等。**[batch_size,len(box),4]** (这一步使用的是`generate_anchor_boxes`方法,不是keras新层AnchorBox,AnchorBox生成的box的最后一个维度是8,已经带了variance)
2. 生成与box同等数量的分类(one-hot形式),初始都是0。 **[batch_size,len(box),n_classes]**
3. 生成与box同等数量的variance。**[batch_size,len(box),4]**
4.连接1+2+3步骤生成的矩阵,其中第一步生成的box重复一次(原本只是模板,只有初始值(为了保证与ssd网络的输出维度一致)),所以尺寸是**[batch_size,len(box),n_classes+4+4+4]**
**匹配模板**
`encode_y`对传入的`ground_truth_labels`
#### 3.3 如何卷积
feature map 都会通过一些小的卷积核操作,得到每一个 default boxes 关于物体类别的21个置信度 $(c_1,c_2 ,\cdots, c_p$ 20个类别和1个背景) 和4偏移 (shape offsets) 。
+ 假设feature map 通道数为 p 卷积核大小统一为 3*3*p (此处p=256)。个人猜想作者为了使得卷积后的feature map与输入尺度保持一致必然有 padding = 1, stride = 1 。 $ \frac{inputFieldSize-kernelSize+2\times padding}{stride}+1 = \frac{5-3+2\times 1 }{1}+1 = 5$
+ 假如feature map 的size 为 m*n, 通道数为 p,使用的卷积核大小为 3*3*p。每个 feature map 上的每个特征点对应 k 个 default boxes,物体的类别数为 c,那么一个feature map就需要使用 k(c+4)个这样的卷积滤波器,最后有 (m*n) *k* (c+4)个输出
参考
https://zhuanlan.zhihu.com/p/24954433