视频来源:https://www.bilibili.com/video/av9770302/?p=15
1 前提概览
生成网络可以做什么? 写诗,画动漫头像。
1.1 Auto-encoder
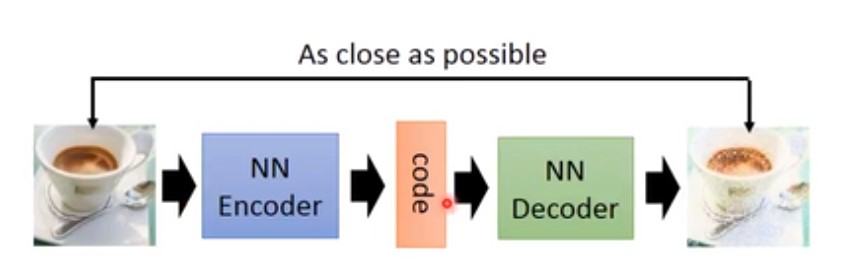
通过encoder将一张图片变成一个 code vector,然后用一个decoder将此code vector 生成一张图像。它们训练时时联合训练,训练完成之后,可以用decoder来生成一张图片。

1.1.1 实例
生成一个手写字生成的decoder,其生成的coder vector假设会2维的,如下:
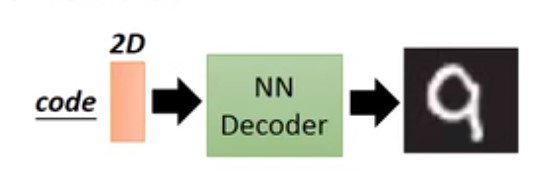
接着,我们输入一个二维向量,假设为 $ [-1.5,0] $,可能生成的手写字是$0$。假设我们输入一个二维向量 $[1.5,0]$生成的手写字可能是$1$。如下图:
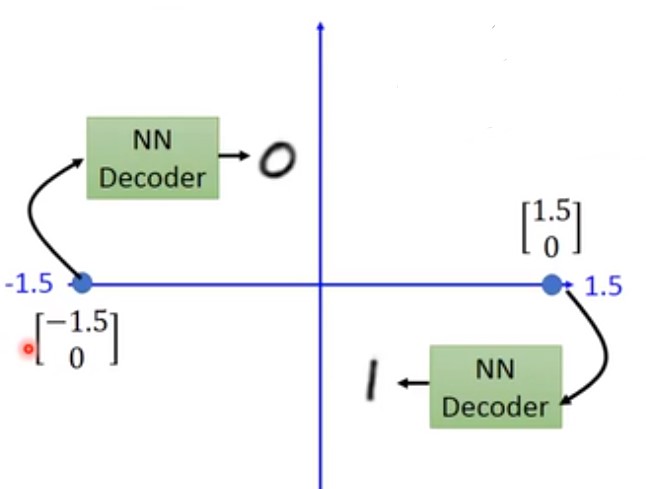
如果,二维向量的值在$ [-1.5,0] $和$ [1.5,0] $之间等距离取值的话,可能得到如下的结果

但是auto-encoder无法生成state of art的结果。
1.2 VAE(Variational Auto-Encoder)
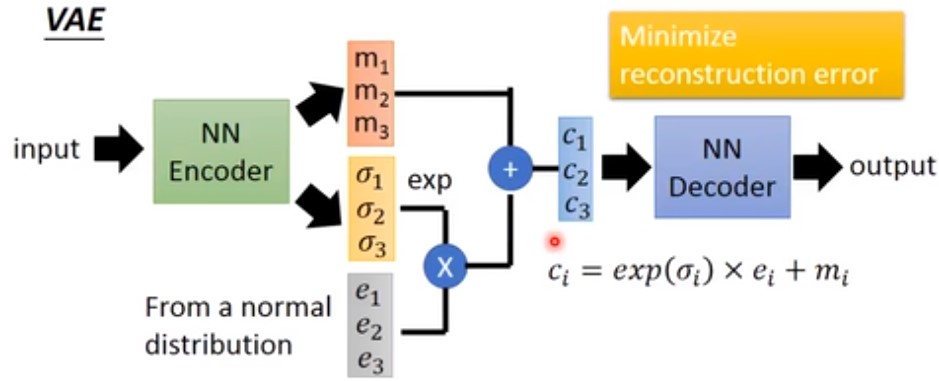
VAE是一个进阶版的auto-encoder,训练的时候,输入一张图片,但是它同时输出三个vector,假设这三个vector都是3维的,如下图:
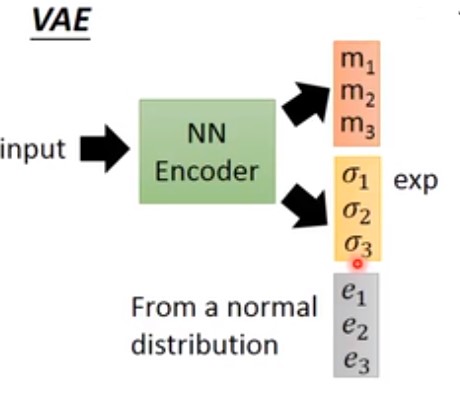
其中的$m_1,m_2,m_3$代表VAE的encoder的输出code,只不过是个三维vector。同时还会生成另外一个三维的vector $\sigma _1,\sigma _2,\sigma _3$,同时会随机从一个符合正态分布的数据集中sample一个三维vector $e_1,e_2,e_3$ (称为noise)。接下来做如下操作:
- 将vector $\sigma _1,\sigma _2,\sigma _3$ 指数化
- 将第一步指数化之后的值与noise vector $e_1,e_2,e_3$ 相乘
- 将生成的code vector $m_1,m_2,m_3$与第二步的结果相加,得到结果 $c_1,c_2,c_3$
再将最后的结果 $c_1,c_2,c_3$ 输入到decoder网络训练,整个过程如下:
1.2.1 VAE的受限条件
在训练VAE时由于添加了额外的项 $\sigma$,则需要添加一个受限条件(假设),即需要最小化:
$$
\sum _{i=1} ^3(exp(\sigma _i)-(1+\sigma _i)+(m_i)^2)
$$
其中 $(m_i)^2$ 可以看做L2 正则,而最小化 $exp(\sigma _i)-(1+\sigma _i)$ 部分即最小化 $\sigma _i$,当它为0时,这部分的值最小。
1.2.2 VAE的问题
我们期望的VAE是它能生成与真实图像越接近越好的图像
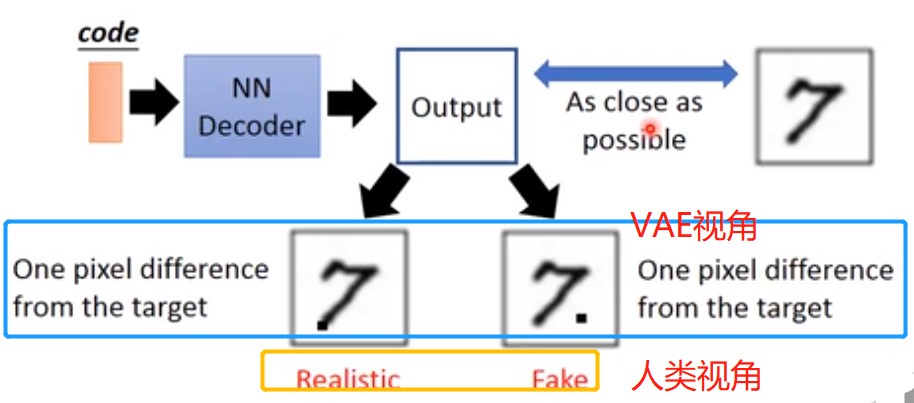
但实际上VAE实际模拟过程与人类的有出入,下图蓝色框代表了两种可能出现的情况。很显然,人类可以分辨出左边是比较接近真实的,右边的不那么接近的(黄色框),但是对于VAE(蓝色框)来说它们在损失函数面前是等价的。
1.3 evolution of generation
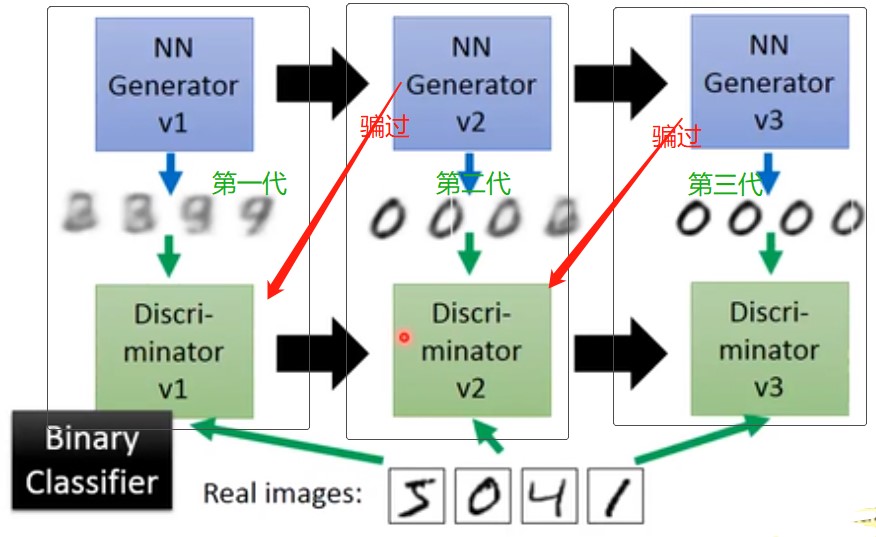
上图是一个示例,分别迭代多次,每次是一对 generator 和 discriminator,不断演化,最后得到较好结果。其中的discriminator是一个二分类器,如果来自真实图像,则输出1,如果来自生成网络则输出0.
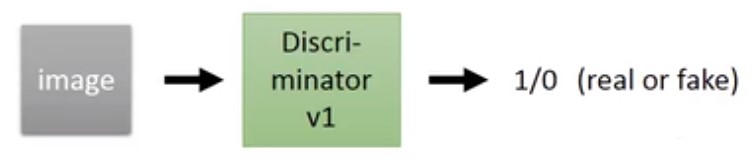
1.3.1 GAN中的Discriminator
Discriminatory本质上是一个二分类分类器,输入一张图片,它会判断该图片是real(1)还是fake(0)。
1.3.2 GAN中的Generator
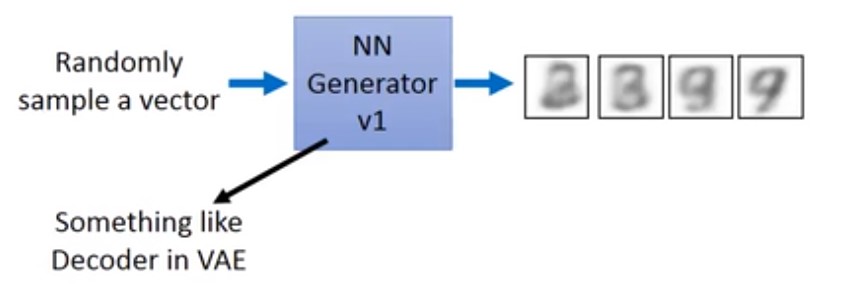
GAN中的Generator与VAE中的decoder类似,输入一个随机的vector,输出一些图片。与VAE不同的是,在训练VAE的时候需要最小化一个重构误差
此处GAN中Generator的架构与VAE一样,只是在训练时方法不一。
首先,我们有个所有参数都是随机产生的generator。此时输入一组参数随机的向量,generator会产生一组假的图像;同时从训练数据集中随机抽取一组真的图像,然后将所有假的图像标签标记为0(negative sample),所有真的图像标记为1(positive sample)
1.3.3 GAN 过程
首先随机输入一组向量给Generator,产生一组图像,Discriminator知道这个是假的图像,会输出一个很低的置信度。
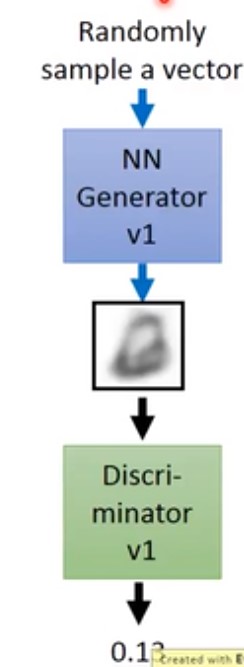
接下来,需要更新generator参数,它会产生的图像让第一代的Discrimintor觉得它是真的图像,输出1。
注意,我们在训练过程中会固定 Discriminator,使用随机梯度更新Generator
二 GAN的核心思路
2.1 最大似然估计
- 给定数据分布 $P_{data}(x)$,此处的$x$就想象成一张图片的所有的像素值串起来。
- 现在我们要找到一个数据分布$P_G(x;\theta)$,它受控于一组参数$\theta$的。
- 其中$P_G(x;\theta)$是一种数据分布,比如可以是高斯混合模型。其中$\theta$代表了高斯分布的期望和方差这两个参数。只不过在GAN中$P_G(x;\theta)$ 是一个 神经网络。
- 那么我们要做的事情就是,找到一个一组参数 $\theta$,使得 $P_G(x;\theta)$的分布与$P_{data}(x)$ 的分布越接近越好。
从 $P_{data}(x)$中抽样${x^1,x^2,…x^m}$。
如果给定参数$\theta$ 那么我们可以计算 $P_G(x^i;\theta)$的值。
似然度:即给定参数$\theta$时,从$P_G(x^i;\theta)$ 中抽样产生 $x^1,x^2,x^3…x^n$的概率。似然度为 $L=\prod ^m _{i=1}P_G(x^i;\theta)$。
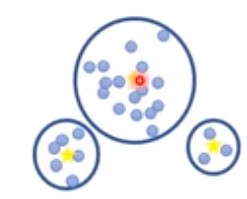
我们要做的其实就找一组参数 $\theta ^*$使得最大化 $L$的似然度。对于高斯混合 模型,参数就是均值、方差,以及混合权重。比如有下图的高斯混合模型,数据有三个高斯分布混合而成,如下:
该分布中均值即上图中三个黄色中心点,方差即三个圆形半径。
$$
\theta ^* = arg \quad max_{\theta} \prod ^m {i=1}P_G(x^i;\theta)=arg\quad max{\theta}\quad log \prod ^m {i=1}P_G(x^i;\theta)\quad 等同于求对数极大值\
= arg \quad max{\theta}\sum ^m_{i=1}logP_G(x^i;\theta)\quad\quad 其中{x^1,x^2,…x^m}都是从 P_{data}(x)中抽样得到的 \
\approx arg\quad max_{\theta}\quad E_{xP_{data}}[logP_G(x;\theta)] \quad\quad 等同于从 P_{x{data}}分布中抽样 x^1,x^2,..x^n 然后计算每个 x^1,x^2,..x^n 使得 log P_G(x;\theta) 最大这件事 \
=arg \quad max_{\theta} \int x P{data}(x)logP_G(x;\theta)dx \
等同于 arg \quad max_{\theta} \int P_{data}(x)logP_G(x;\theta)dx-\int xP{data}(x)log P_{data}dx \
=arg\quad min_{\theta}\quad KL(P_{data}(x)||P_G(x;\theta)) \quad 【KL散度】
$$
在GAN之前,高斯混合模型生成的图像非常模糊,因为高斯混合模型无法真正模拟图像数据分布。
2.2 将 $P_G(x;\theta)$ 换成一个神经网络
此时的GAN结构如下,输入通常为一个简单的 高斯分布的向量。经过神经网络 $G(z)$ 之后输出x
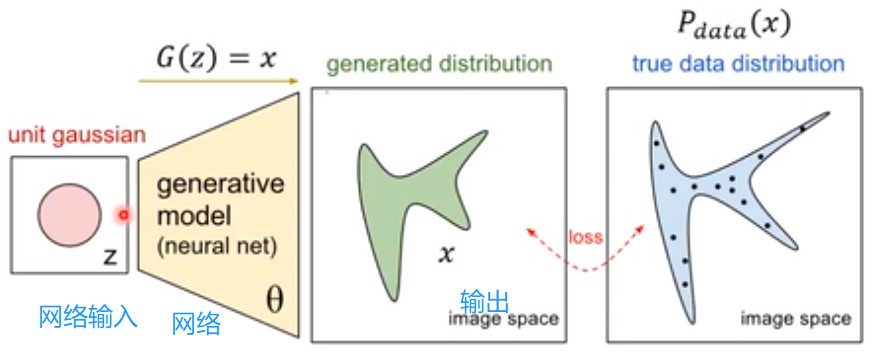
关于神经网络 $G(z)$ 的函数表达式可以表示为: $P_G(x)=\int xP{prior}(z)I_{[G(z)=x]}dz$ 。该公式的通俗理解是,假设$G(z)$参数已经固定(即网络参数固定),从该网络中取样得到x的概率等于,对所有可能的z取积分,乘以z出现的概率($P_{prior}(z)$),同时每个z经过函数$G(z)$之后生成x,该x是否即为当前正在考量的x,此处由函数$I_{G(z)=x}$判定,如果等同则为1,否则为0。
当前问题是,如果以这种方式计算。难以计算,给定x,即便我们知道输入分布z的参数,但是由于神经网络极其复杂,要想计算由网络生成x的概率会很困难。 在无法计算似然度的情况下,无法调整参数$\theta$使得网络输出x接近真实数据分布。这个就是GAN的共享。
2.3 GAN的基本介绍
- Generator G
- G是一个函数,输入为Z,输出为x
- 给定先验分布 $P_{prior}(z)$ ,又得知函数G,我们可以定义一个概率分布 $P_G(x)$
- Discriminator D
- D是一个函数,输入为x,输出为标量。
- Discriminator D的作用就是衡量 $P_G(x)$和 $P_{data}(x)$的差异
- 有一个函数 $V(G,D)$,我们要找的最好的G。 $G^* = arg\quad min_G\quad max_D\quad V(G,D)$
2.3.1 如何理解 $G^* = arg\quad min_G\quad max_D\quad V(G,D)$
我们先看最右边的 $max_D\quad V(G,D)$ 部分。它的意思是选择使得 $V(G,D)$最大的 D,假设我们只有三个可能的G($G_1,G_2,G_3$,如下图),实际上由于G是一个神经网络,所以它有无数种可能。
下图中,分别对于不同可能的G,改变D,可以得到不同的 $V(G,D)$。对于$G_1,G_2,G_3$,$max_DV(G,D)$(最大值)就是下图中,红色点的值。
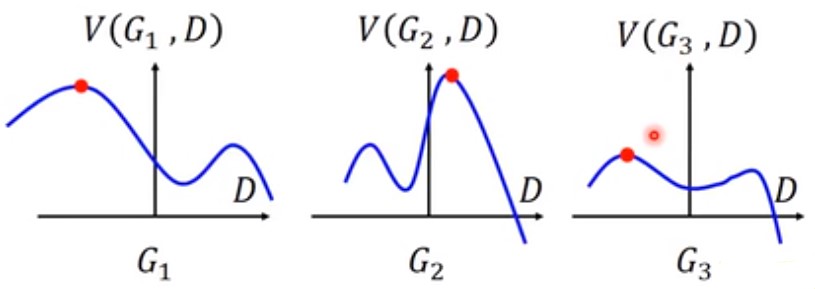
接下来再去寻找一个$G^* $使得 $max_DV(G,D)$最小的G,可以从上图(红色点)中看到,对于 $G_1,G_2,G_3$其最大值,在为$G_3$时它的最大值最小。
2.3.2 关于函数 V的定义
$V= E_{xP_{data}}[logD(x)]+E_{xP_G}[log(1-D(x))]$ ,先不用考虑此公式如何得来。
对于给定的G,$max_DV(G,D)$评估的是 $P_G$和$P_{data}$之间的差异,所以我们要寻找的是那个能使得 $P_G$和$P_{data}$差异最小的 $P_G$($P_{data}$固定)。
对于给定G,最优的$D^*$是可以最大化V的。其中V的形式如下:
$$
V=E_{xP_{data}}[logD(x)]+E_{xP_G}[log(1-D(x))]\
=\int xP{data}(x)logD(x)dx+\int _xP_G(x)log(1-D(x))dx \quad \quad 期望等于概率的积分\
=\int x[P{data}logD(x)+P_G(x)log(1-D(x))]dx\quad\quad 都是对x的积分,相同部分放一起
$$对于给定$x$,最优化的V等价于最大化上式中括号中的
$$
P_{data}logD(x)+P_G(x)log(1-D(x)) \
a\quad\quad\quad D\quad\quad b\quad\quad\quad D\quad\quad \
给定x,P_{data}和P_G都是常量
$$找到$D^*$能够最大化: $f(D)=alog(D)+blog(1-D)$,对该式子求极值的方法就是下面求导,取0得到。
$$
\frac{df(D)}{dD}=a\times \frac{1}{D}+b\times \frac{1}{1-D}\times (-1)=0 \
\rightarrow a\times \frac{1}{D}=b\times \frac{1}{1-D} \
\rightarrow a\times (1-D^*)=b\times D* \
\rightarrow D^* = \frac{a}{a+b} \quad\quad 再把a,b代回来得到\
\rightarrow D^*(x)=\frac{P_{data(x)}}{P_{data}(x)+P_G(x)}
$$
将各个$D^*$ 显现在图中,如下:
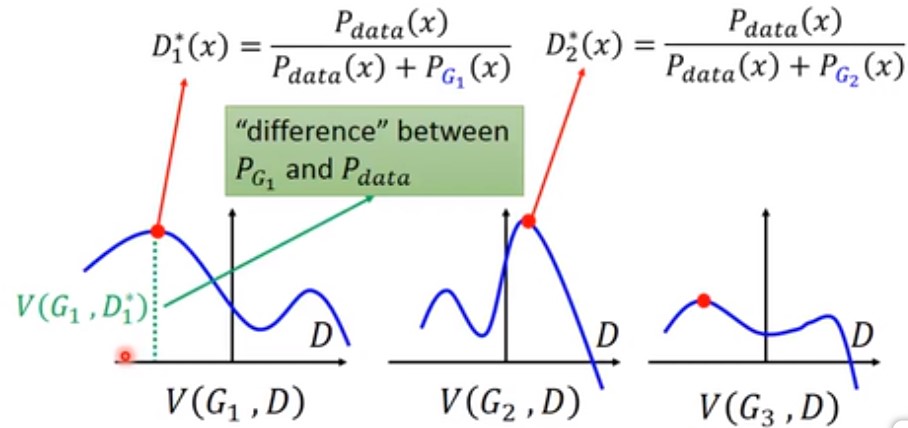
红色顶点处即,不同的$G$,取得最大D的值。该点到水平轴(D)的距离就是$V(G,D)$的值,也即$P_{G_1}$和$P_{data}$的差异。
由上面的推导可知 $D^*(x)=\frac{P_{data(x)}}{P_{data}(x)+P_G(x)}$。而$V(G,D)=E_{xP_{data}}[logD(x)]+E_{xP_G[log(1-D(x))]}$。那么,其实我们带入得到:
$$
D^*(x)=\frac{P_{data(x)}}{P_{data}(x)+P_G(x)} \
=E_{xP_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}] + E_{xP_G}[log\frac{P_G(x)}{P_{data}(x)+P_G}] \quad 将求期望转换为求积分\
\rightarrow \int x log\frac{P{data}(x)}{P_{data}(x)+P_G(x)}dx +\int x P_G(x)log \frac{P_G(x)}{P{data}(x)+P_G(x)}dx \
下面就开始推导 KL散度了,这里就不推导了。推导完也记不住,也看不懂
$$
那么对于给定G, $max DV(G,D)$可以看做计算 $-2log2+2JSD(P{data}(x)||P_G(x))$(其中$JSD(P_{data}(x)||P_G(x))$用以衡量$P_G和P_{data}$之间的差异度,是从上面的推导推导而来)。$JSD(P_{data}(x)||P_G(x))$的取值范围,最小为 $0$,即$P_G$和$P_{data}$完全重合,最小值为$log2$即$P_G$和$P_{data}$完全不存在交集。所以$max _DV(G,D)$的取值范围为 $[-2log2,0]$
那么,那个G才是使得$max DV(G,D)$ 最小的值呢? 只有当 $P_G=P{data}$
2.3.3 具体算法
算法可以按照如下步骤循环:
给定一个初始的 $G_0$
根据$G_0$ 找到一个 $D^* _0$使得它可以最大化 $V(G_0,D)$
- 其中 $V(G_0,D^* 0)$ 是$P{data}$和 $P_{G_0}(x)$之间的JS差异。
- 下一步,我们需要找一个新的 $G$,假若为 $G_1$。它必须使得$P_{data}$和 $P_{G_0}(x)$之间的JS差异减小。可以通过求梯度的方法,
$ \theta _G\leftarrow \theta_G -\lambda \frac{\partial V(G,D^* _0)}{\partial \theta _G}$ 。可以通过此公式计算得到新的 $G_1$
用新的 $G_1$计算$P_{data}$和 $P_{G_1}(x)$之间的JS差异
再找下一个$G_2$,使用同样的方式…
重复,不断去寻找新的G
2.3.4 实际如何操作
我们的loss函数是 $V=E_{xP_{data}}[logD(x)]+E_{xP_G}[log(1-D(x))]$。在上面的推导过程中,我们是假定可以对$P_{data}$求积分的,但是实际情况是,{P_{data}}是所有可能图像的分布,是不可积分的。所以,我们做如下逼近。
通过从 $P_{data}(x)$中抽样 ${x^1,x^2,x^3,…x^m}$来毕竟 $P_{data}$可能的数据分布,同时从generator $P_G(x)$中也抽样 $\tilde x^1,\tilde x^2,..\tilde x^m$。
那么我们求上面的$V=E_{x
P_{data}}[logD(x)]+E_{xP_G}[log(1-D(x))]$也等同于求一个 $\tilde V=\frac{1}{m}\sum ^m_{i=1}logD(x^i)+\frac{1}{m}\sum ^m_{i=1}log(1-D(\tilde x^i))$ 。此式可以看做一个对二分类分类器的交叉熵损失函数。- 比如一个二分类分类器,假若其输出为$D(x)$,那么我们就需要最小化其交叉熵,我们会这么做
- 如果$x$是正样本,那么就需要最小化 $-logD(x)$
- 如果$x$是负样本,那么就需要最小化 $-log(1-D(x))$
再回过来,D是一个参数为$\theta$的二分类的分类器。我们从 $P_{data}(x)$中抽取 $x^1,x^2,…x^m$作为正样本,从$P_G$中抽样 $\tilde x^1,\tilde x^2,…\tilde x^m$作为负样本。以上面讨论的结论可以将最大化$V$变成最小化 $L=-\frac{1}{m}\sum^m {i=1}logD(x^i)-\frac{1}{m}\sum ^m{i=1}log(1-D(\tilde x^i))$
2.4 GAN完整算法
- 在每次算法迭代过程中,都会更新Discriminator和Generator
我们先看看学习Discriminator 部分,一般会重复K次,一次无法找到全局最优参数。
- 从数据分布 $P_{data}(x)$中抽样 ${x^1,x^2,…x^m}$
- 从先验分布$P_{prior}(z)$中随机抽取噪声数据${z^1,z^2,…z^m}$。注意此处的先验分布只是个普通的正态分布
- 将先验分布抽样得到的${z^1,z^2,…z^m}$喂入$\tilde x^i=G(z^1)$,获取一批生成数据 ${\tilde x^1,\tilde x^2,…\tilde x^m}$
- 更新discriminator的参数 $\theta _d$,可以使得下式最大
- $\tilde V = \frac{1}{m}\sum ^m_{i=1}logD(x^1)+\frac{1}{m}\sum ^m _{i=1}log(1-D(\tilde x^1))$
- 使用梯度下降方法计算 $\theta _d\leftarrow \theta _d+\lambda \nabla \tilde V(\theta _d)$
再来看训练Generator部分,下面的部分通常只会更新一次。generator不能更新太多,否则会导致JS差异度无法下降(generator已经以假乱真了)。
从先验分布$P_{prior}(z)$中随机抽取噪声数据${z^1,z^2,…z^m}$。此处的随机噪声数据可以与上面训练Discriminator部分的随机样本值一样,也可以不一样
更新Generator的参数 $\theta _g$使得下式最小
- $\tilde V = \frac{1}{m}\sum^m {i=1}logD(x^i)+\frac{1}{m}\sum ^m{i=1}(1-D(G(z^i)))$ 。可以看到此式,前半部分跟Generator无关
- 再用梯度下降法去更新 Generator的参数:$\theta _g-leftarrow \theta _g+\lambda \nabla \tilde V(\theta _g)$
3 实际如何实现GAN
3.1 真实实现中,Generator的目标函数
从上面的讨论中,我们可以看到Generator会使得式子 $V= E_{xP_{data}}[logD(x)]+E_{x-P_G}[log(1-D(x))]$的值最小。省略前面的(与generator无关),只看$E_{x~-P_G}[log(1-D(x))]$这部分,目标函数理论上应该是最小化此式,但是我们可以分别看看 $-log(D(x))$和 $log(1-D(x))$曲线,如下图(上面蓝色的为$-log(D(x))$,下面红色的为$log(1-D(x))$):
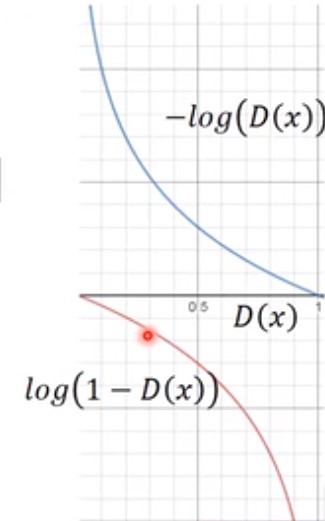
观察需要最小化的 $log(1-D(x))$,在$D(x)$很小时,该曲线很平滑,在$D(x)$很大时该曲线很陡峭。 $D(x)$很小意味着,由Generator产生出来的x无法骗过Discriminator,Discriminator可以很容易认出。也即在训练的初始步骤,由generator产生的样本都集中在平滑部分,此时的$log(1-D(x))$微分值很小,训练变得缓慢。此时,我们可以修改目标函数为
$$
v= E_{x~P_G}[-log(D(x))]
$$
此式子效果等同于$log(1-D(x))$,同时可以快速训练,在初始步骤微分值很大,在后续步骤变得很小,比较符合训练期待。
3.2 如何评估JS divergence(差异)
我们将discriminator的loss就是来衡量JS divegence,loss越大,divergence越大
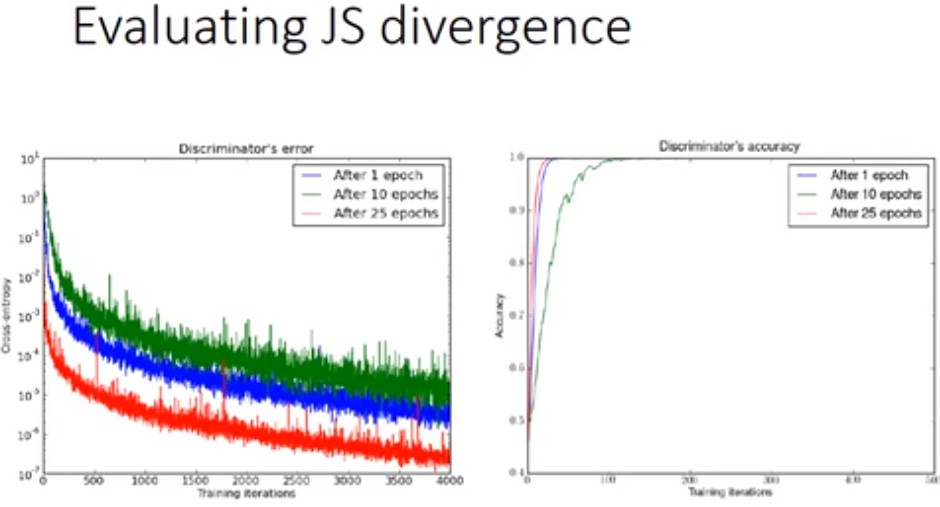
图中分别衡量的三个Generator,分别训练了1个epoches,10个epoches,25个epoches。其中训练了25个epoches的generator已经几乎可以state of art了,但是用这些Generator去训练discriminator时,discriminator依然有十分高的准确率。
我们先看看目标损失函数 $max DV(G,D)=-2log2+2JSD(P{data}(x)||P_G(x))$ 导致这个问题的主要原因有以下几点
- 我们在训练和调整到的时候,不是真正用积分去计算,而是通过抽样来拟合。现在假设我们有红色和蓝色两个椭圆的数据点分布,如下,但是因为我们是使用抽样的方式来代表数据分布:
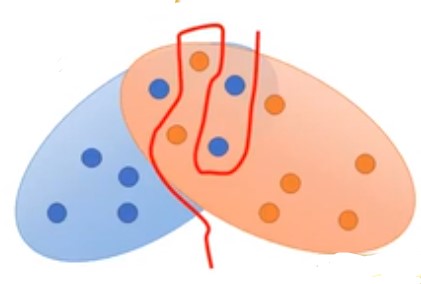
即便Generator产生的数据样本与真实样本之间有重叠,但是由于Discriminator比较强,所以它依然能找到一条曲线将红色点和蓝色点区分开。如何解决这个问题?
- 使得discriminator 变弱一点,少更新,加dropout。但是一个弱discriminator将导致JS divergence无法计算。
- $P_G$和$P_{data}$都是高维空间数据,现在假设它们都是二维空间的,那么 $P_G$和$P_{data}$可以看做二维空间里面的两条直线,那么这两条之间的交集非常小,几乎趋近于零(如下两条直线)。

所以真实$P_G$和$P_{data}$的情况可能像下面这样演化:
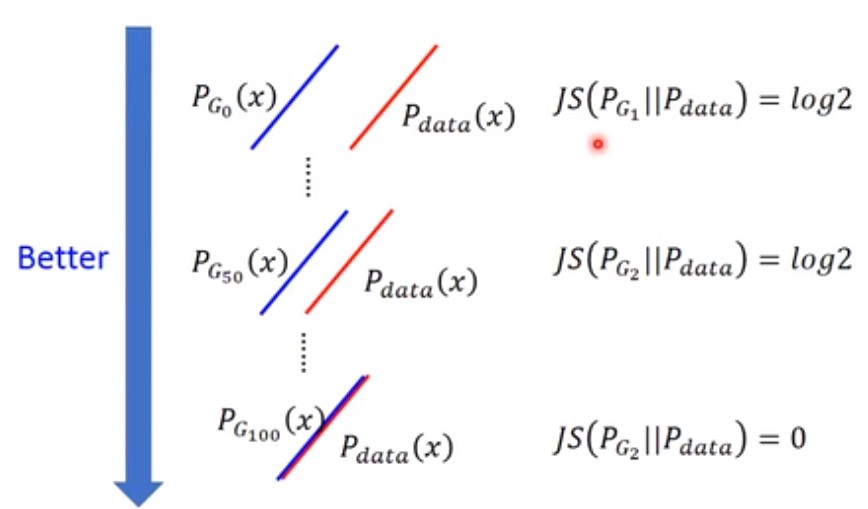
可以看到在$P_G_0$和$P_G_{50}$…到$P_G_{100}$之前,JS divergence都是log2,GAN没有演化的动力。
3.3 如何解决GAN无法优化的问题
- 加入噪音数据。在discriminator的输入中加入一些人工噪音数据
- 训练Discriminator时,将其label加噪音。比如有张图片是positive,现在随机替换图像的部分内容为噪音
加入噪音数据之后,原本交集非常少$P_G$和$P_{data}$就可能会拓宽。如下:

注意:噪音数据要随着训练的推荐,逐步减小
4 mode collapse
比如有真实的数据分布为蓝色,而generator生成的数据分布为红色。如下左图,右边是对应生成的图像。
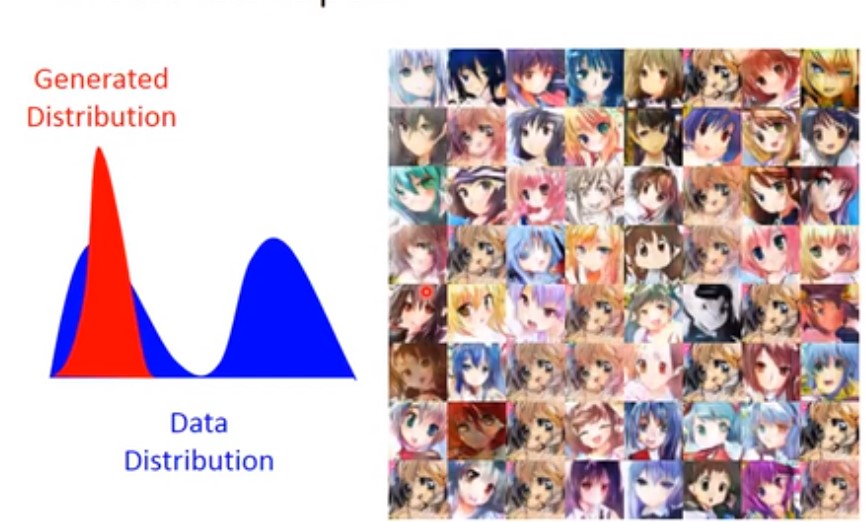
现在问题是,我们只知道GAN生成了的数据,无法知道GAN没有生成的数据。
假设当前$P_{data}$的数据分布如下,为8个黑点。
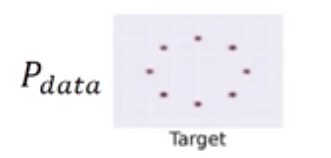
但是,我们训练过程中会出现不一致的情况。比如,我们期望$P_G$可以慢慢去覆盖$P_{data}$,但是实际训练时$P_G$一直只产生一个数据分布,不断去调整,但始终无法覆盖所有的$P_{data}$
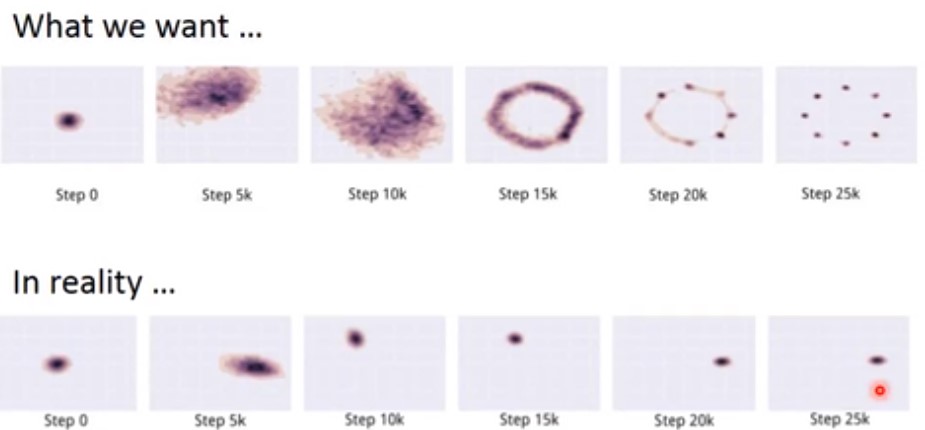
可能的原因是之前的损失函数定义,即KL divergence定义有误。下图左边代表了原始的损失函数定义
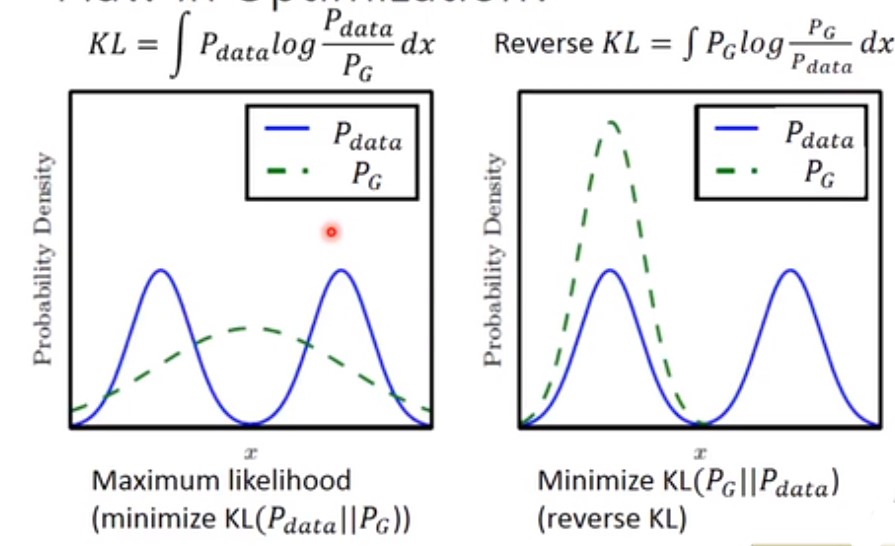
其中 $KL= \int P_{data}log\frac{P_{data}}{P_G}dx$,当$P_{data}$有值,而$P_G$没有值的时候,该函数将取无穷大的值。所以此时GAN会尽力去覆盖尽可能多的$P_{data}$的数据。
而看上图右边,KL divergence的倒数,$Reverse KL= \int P_{data}log\frac{P_G}{P_{data}}dx$。此时当$P_G$有值,而$P_{data}$没有值得时候函数取值会趋近无穷大,此时为了避免出现这种情况,$P_G$会尽可能拟合一个数据分布(假设真实的$P_{data}$由多个分布组成的话)。
5 condintional GAN
与GAN不同的时,我们想生成制定的东西,此时的Generator输入就不止一个先验分布(正态分布)了。如下:
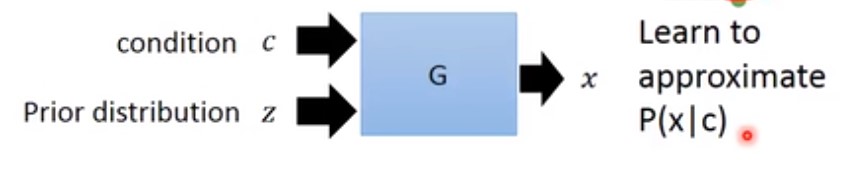
但此时可能会出现一个问题,generator可能会无视先验分布($P_Z$),generator会觉得先验分布只是个噪音数据,解决办法是在generator里面添加 dropout。
此时训练Discriminator也不一样,它的输入不再是一张图片,而是一张图片以及对应的描述,而对应的label则根据正负样本区别对待。
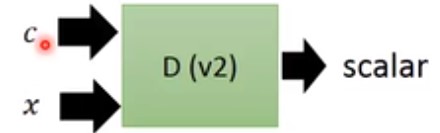
- 正样本: $(\hat c,\hat x)$,其中$\hat c$为图像真实描述,$\hat x$为真实图像。
- 负样本: $(\hat c,G(\hat c)),(\hat c’,x)$。其中$\hat c$为真正的图像描述,而$G(\hat c)为对generator输入$\hat c$时生成的图像$。同时要有另外一种fake sample,给discriminator真实的图像,但是给错误的描述。比如此处的$\hat x$为真实图像,但是$\hat c’$为错误描述。