1 常规卷积
不知道常规卷积计算的,可以去各种卷积的在线演示看看。假设我们有个尺寸为$12\times 12\times 3$的图像,其中的3位RGB三通道。需要执行一个$5\times 5$的卷积,$stride=1,padding=valid$,所以卷积之后的feature map尺寸为$8\times 8(12-5+1=8)$。
由于图像是三通道,所以我们的卷积核也必须是三通道的。所以每次卷积核在图像上移动一次的时候的计算的不是简单的$5\times 5=25$,实际上是$5\times 5\times 3=75$次乘法操作。即,实际是每次对25个像素矩阵做乘法计算,然后输出一个数值。经过$5\times 5\times 5\times 3$的卷积核之后,$12\times 12\times 3$的图像变成了$$8\times 8\times 1$的特征图。
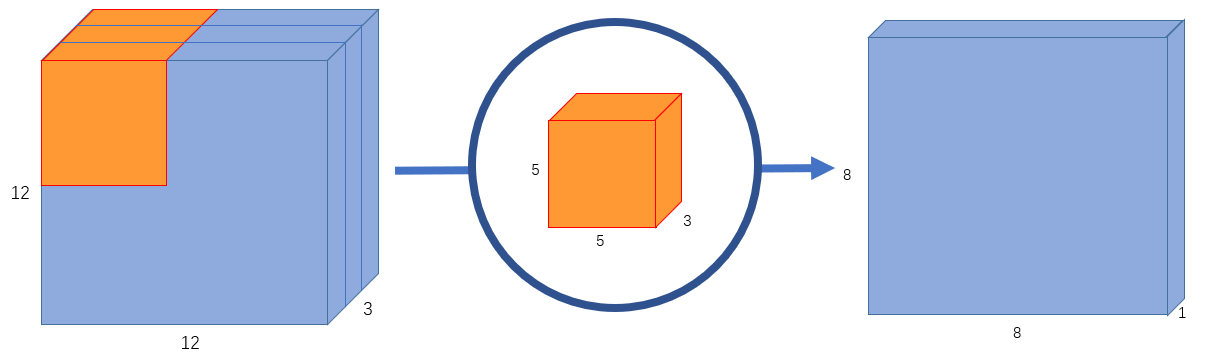
如果想增加输出特征图的通道数,比如说增加到256,使用256个卷积核,然后把所有结果堆叠起来即可。
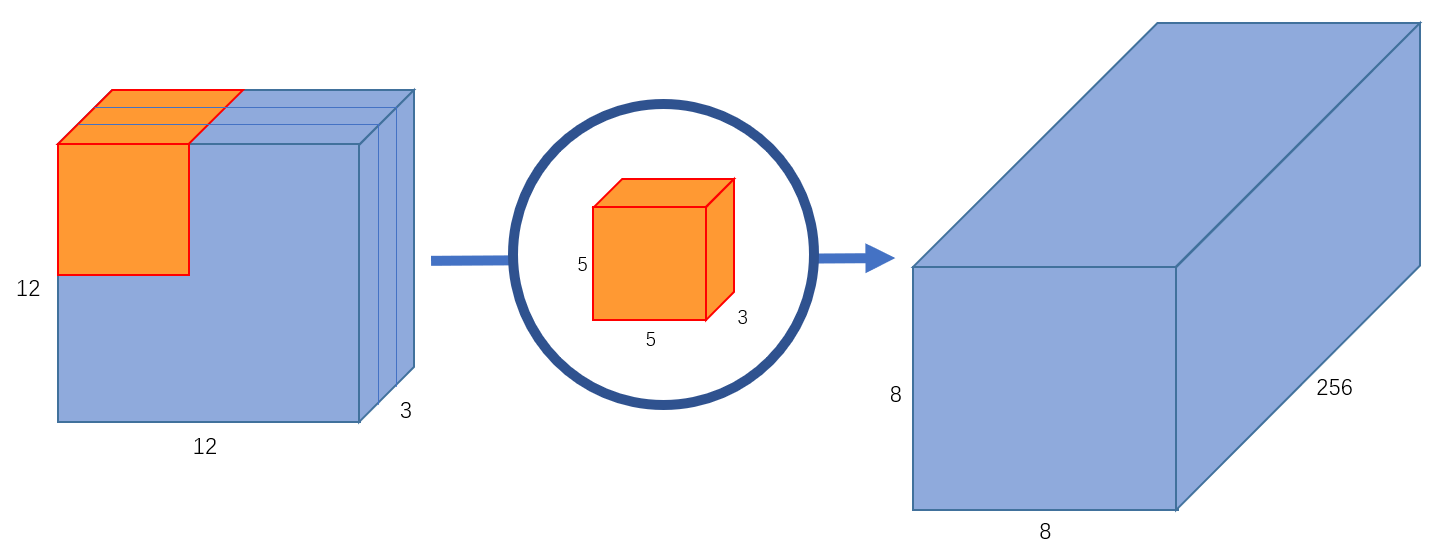
很显然,这并非矩阵乘法(不是用一整张图与卷积核相乘),而是每次单独地与图像的一部分相乘。
2 深度分离卷积
深度分离卷积分为两部分
- 深度卷积
- 逐点卷积
2.1 逐通道卷积
假设图像依然是$12\times 12\times 3$,这次使用的是3个$5\times 5\times 1$的卷积。
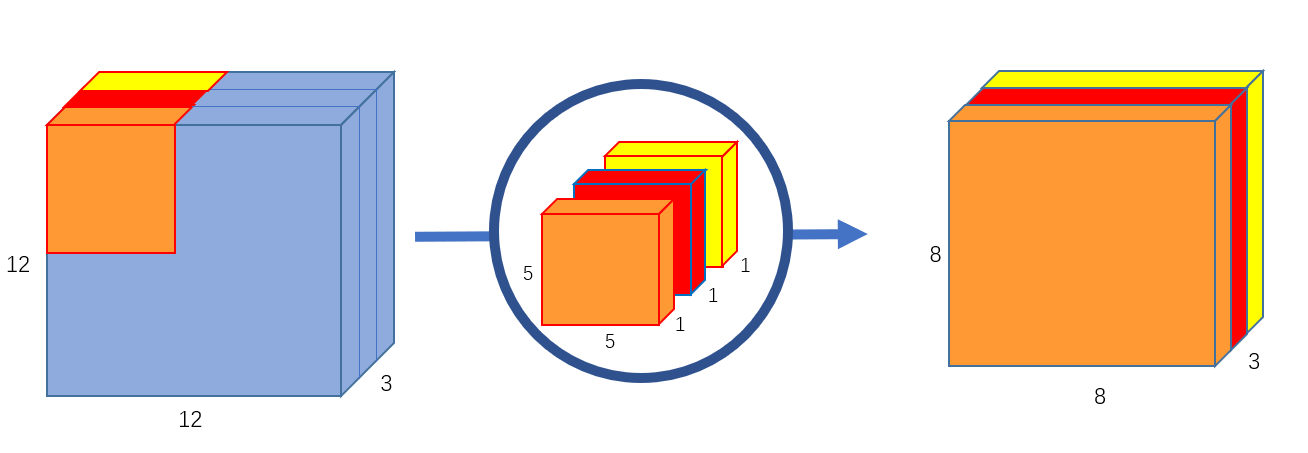
每个$5\times 5\times 1$卷积迭代图像的一个通道,即每次都是25个像素的点乘,然后输出一个$8\times 8\times 1$的图像
2.2 逐点卷积
前面,我们把$12\times 12\times 3$的图像卷积变成了$8\times 8\times 3$的图像,现在我们需要增加每个图像的通道数。
逐点卷积这个叫法源于它使用的是$1\times 1$的卷积核,你可以看做它迭代的计算图像上每个像素点。它有与输入图像同样多的通道数,当前示例中的通道数为3。因此,在$8\times 8\times 3$的图像上迭代$1\times 1\times 3$,可以得到一个$8\times 8\times 1$的特征图像。
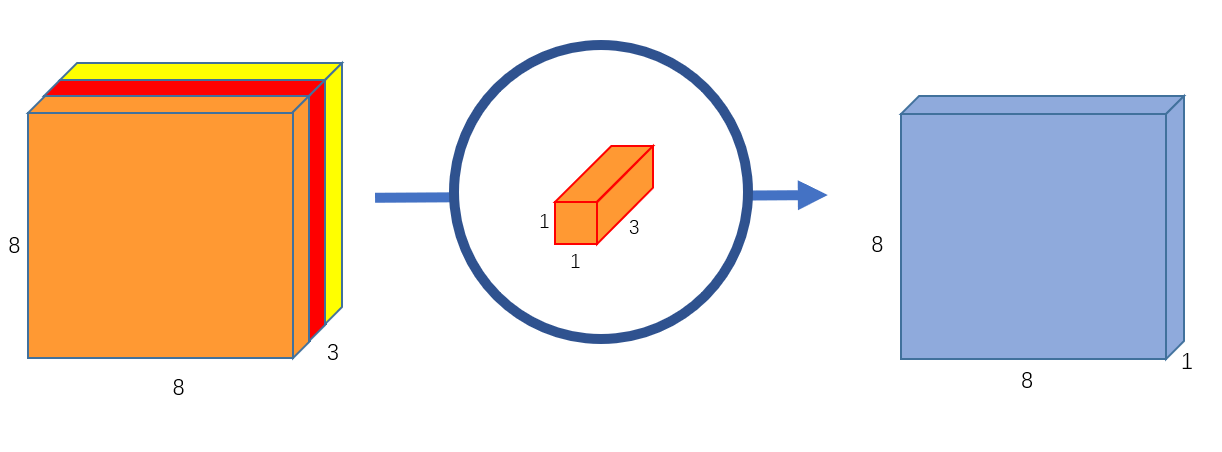
我们也可以使用256个$1\times 1\times 3$的卷积核,每个卷积之后输出输出一个$8\times 8\times 1$图像,堆叠起来就有$8\times 8\times 256$的特征图
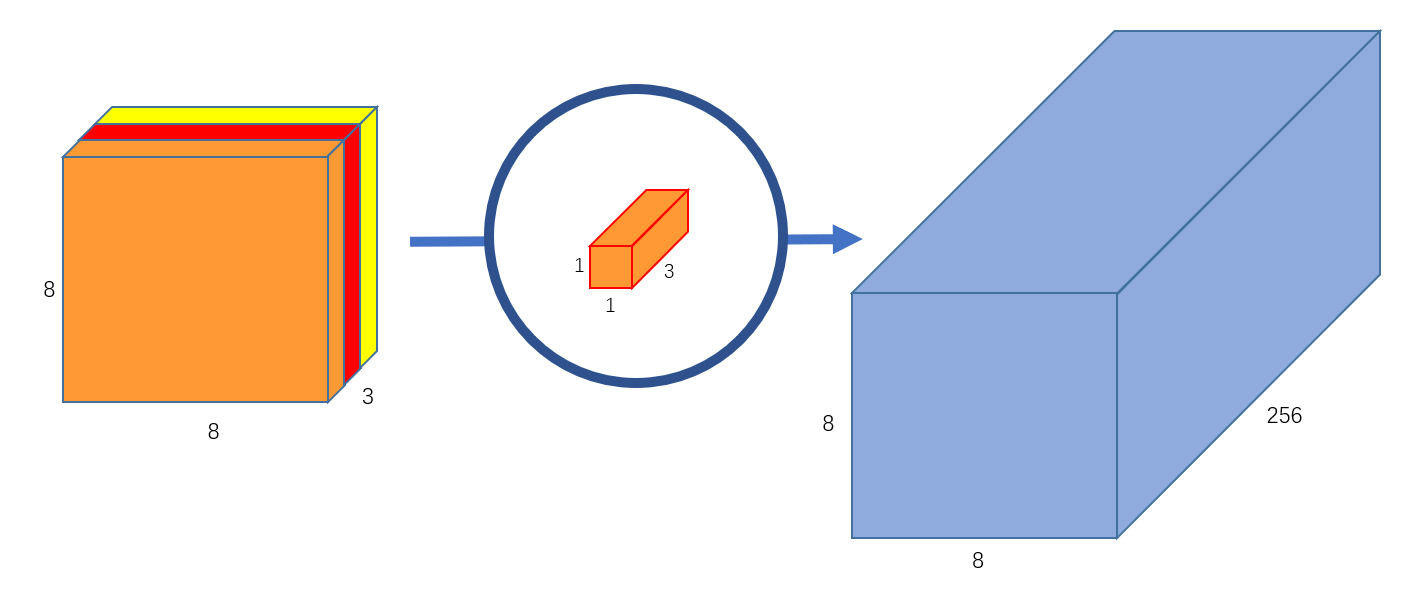
我们将一个卷积操作分离成了逐通道卷积和逐点卷积。更直观的说明:
- 原始的卷积的计算步骤: $12\times 12\times 3–5\times 5\times 3\times 256\rightarrow 12\times 12\times 256$
- 深度分离卷积计算步骤: $12\times 12\times 3–5\times 5\times 1\times 1\rightarrow 1\times 1\times 3\times 256\rightarrow 12\times 12\times 256$
2.3 深度分离卷积的意义是什么呢
主要是减少计算量,加快计算过程。
- 原始的卷积的计算过程。256个$5\times 5\times 3$的卷积,移动$8\times 8$次。总计算量是 $256\times 3\times 5\times 5\times 8\times 8=1228800$次乘法操作
- 分离卷积之后。使用3个$5\times 5\times 1$的卷积,移动$8\times 8$次,是$3\times 5\times 5\times 8\times 8=4800$次乘法。在逐像素卷积步骤,有256个$1\times 1$移动$8\times 8$次,总共$256\times 1\times 1\times 3\times 8\times 8=49512$次乘法。加起来总共$53952$次乘法。
3 总结
主要区别是什么?常规卷积中,我们对图像进行了245次转换,每次转换使用$5\times 5\times 3 \times 8\times 8=4800$次乘法。在分离卷积中,我们真正转换操作只进行在逐通道卷积上了一次,然后仅仅将其拉长到256个通道上。此时已经没有对图像做转换。
4 空间分离卷积
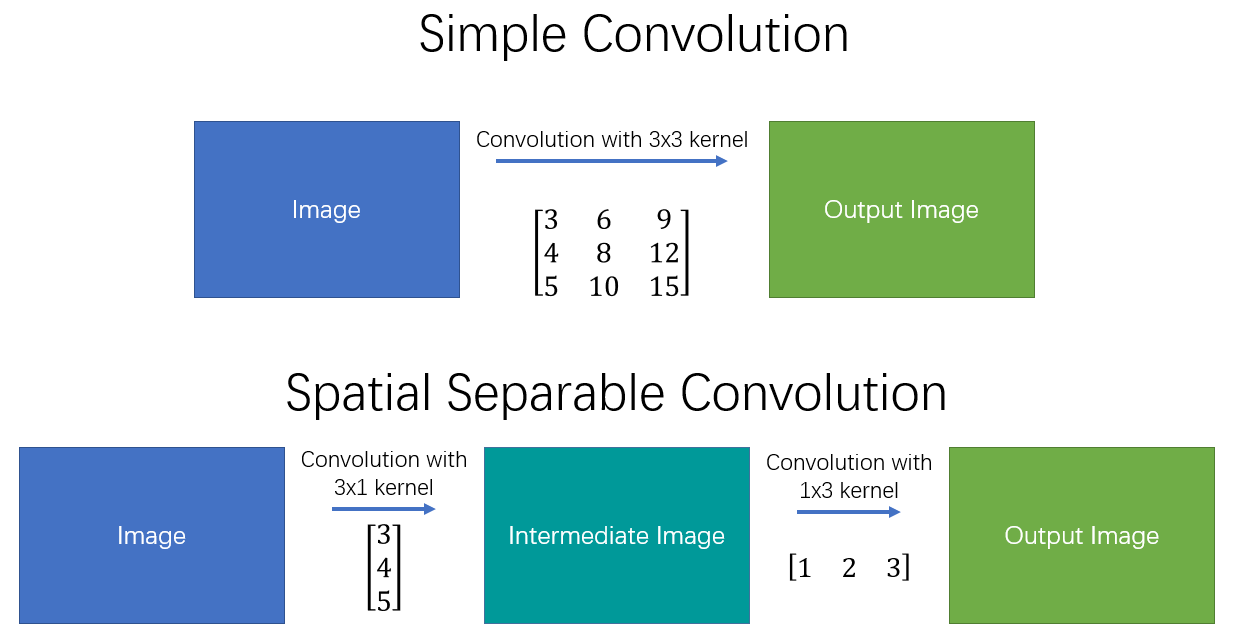
空间分离卷积的思想很简单,就是把一个二维卷积分解成2个一维卷积,比如说一个$3\times 3$的卷积分离成一个$3\times 1$和一个$1\times 3$的卷积。如下
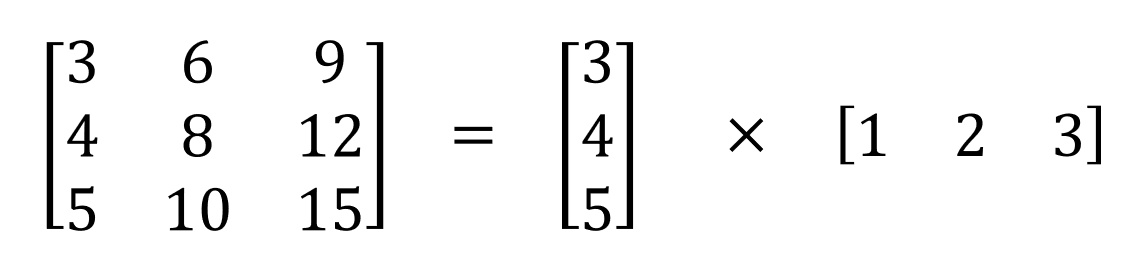
对应在图像上的计算步骤,与常规卷积相比多了一个中间图像
最有名的空间分离卷积是Sobel卷积算子,
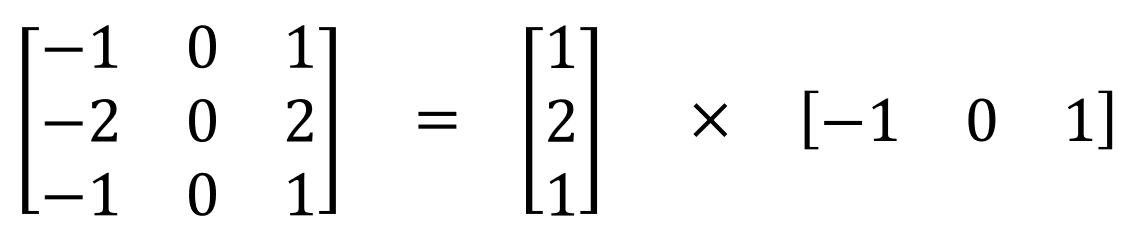
空间分离卷积的局限性在于,不是所有的卷积都可以这么分解。影响了其普适性。