本文翻译自: https://medium.com/@yu4u/why-mobilenet-and-its-variants-e-g-shufflenet-are-fast-1c7048b9618d
1 高效网络中所使用的Block模块
假设我们有如下的卷积过程:
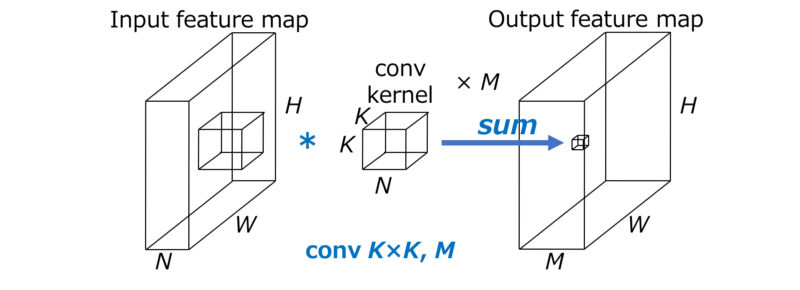
假设$H\times W$代表了上一层的输出空间尺寸,即当前卷积的特征输入尺寸,其中的N代表了输入通道,$K\times K$代表了卷积核的尺寸,M代表了输出的特征通道数。这样一来,标准卷积的计算量是$H\times W\times N\times K\times K\times M$。
此处需要注意的是标准卷积的计算消耗与下面三点是成比例的:
- 前一层的输出特征的空间尺寸$H\times W$,即当前卷积的输入尺寸。
- 卷积核尺寸$K\times K$
- 输入特征通道数N、输出的特征通道数M。
当卷积同时在空间(宽度)以及通道(深度)上做卷积操作时,上述计算消耗都是必须的。CNN可以被以下的卷积分解方法来加速卷积。
1.2 卷积
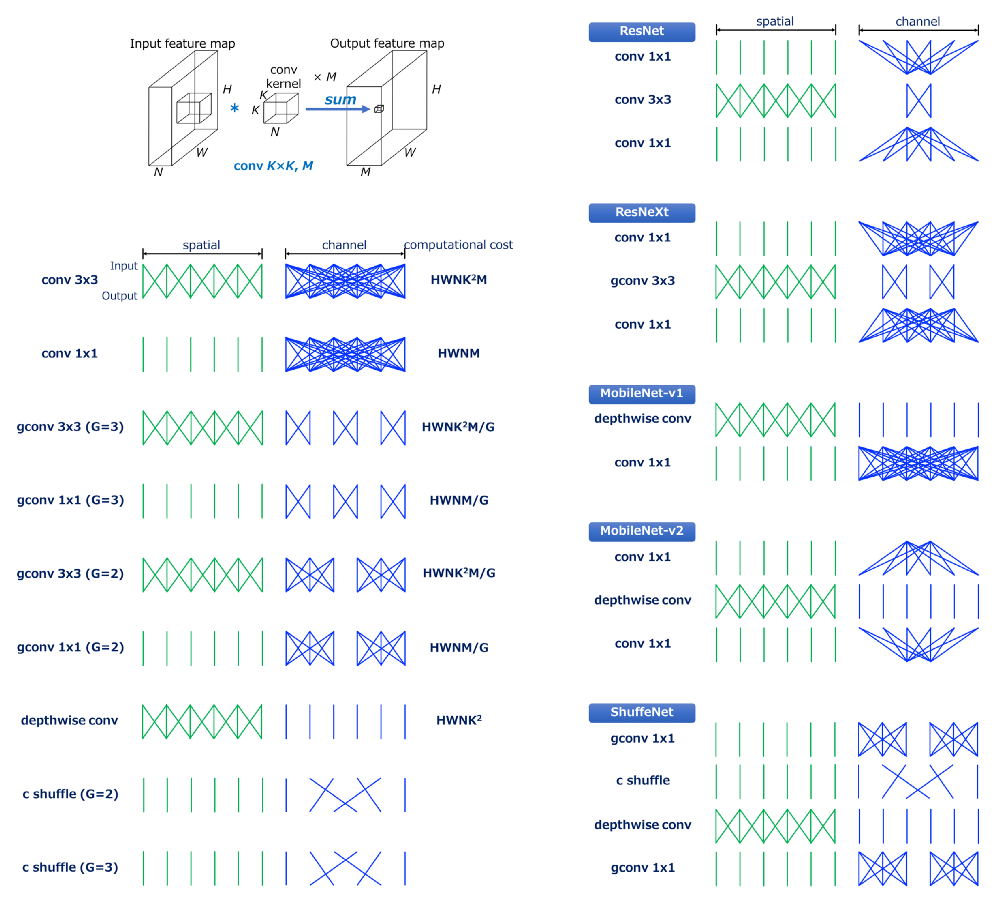
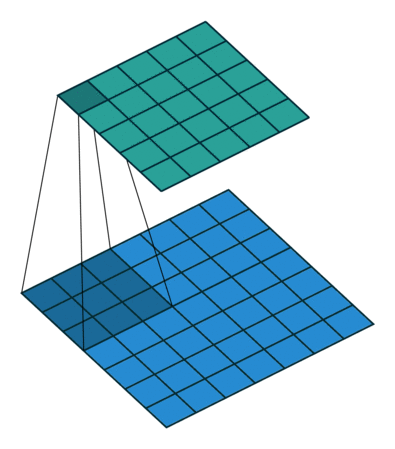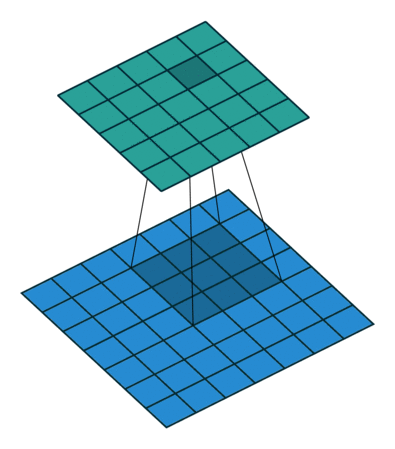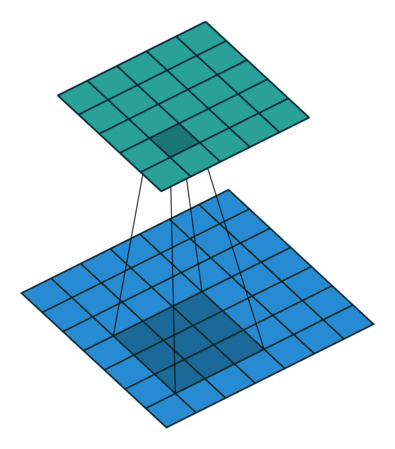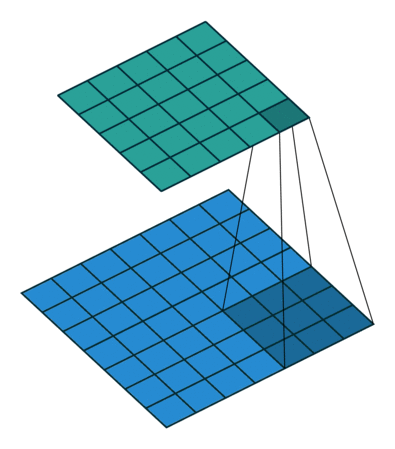
我们在输入输出之间连线来可视化输入输出之间的依赖,连线的数量大概地展示卷积分别在空间和通道域上的计算消耗。

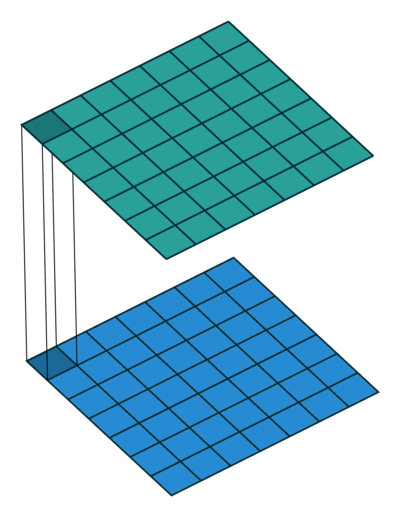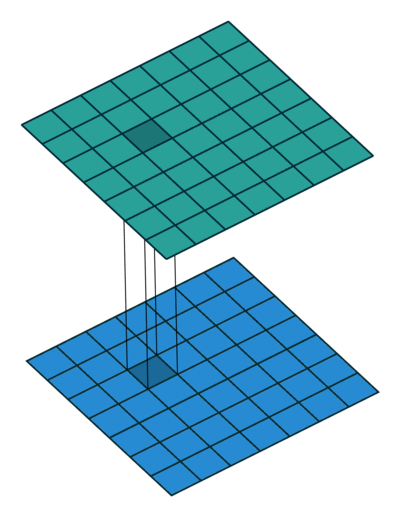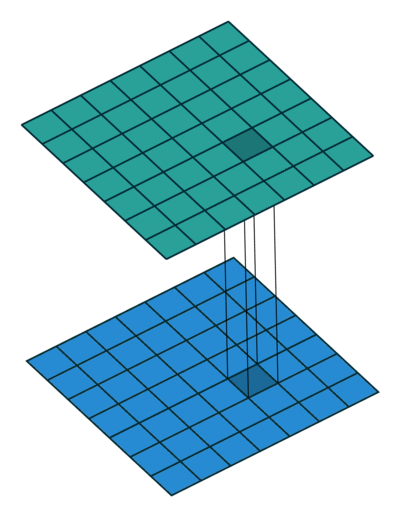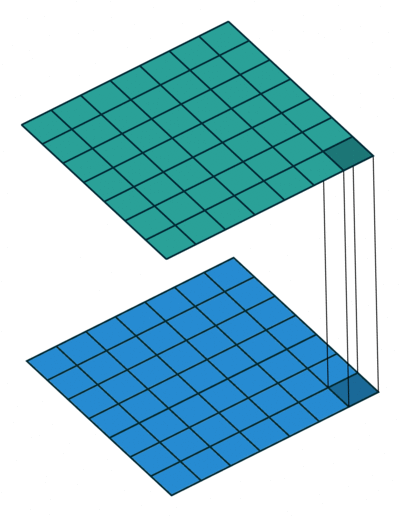
例如,常见的$3\times3$卷积可以向上图展示所示。我们可以看到**输入和输出在空间尺度上是局部连接的(上图左),而在通道尺度上是全连接(上图右)**。接下来我们看$1\times1$卷积,也即点卷积,用来改变通道数,如下图。其卷积计算消耗是$H\times W\times N\times M$,因为卷积核是$1\times1$,导致计算量只有$3\times3$的1/9。此卷积用来混杂通道之间的信息。

1.2.1 1x1卷积的效果
- 先看看$3\times 3$卷积效果
- 再看$1\times 1$卷积效果
1.3 分组卷积
分组卷积为卷积的变种,特点是输入特征的通道数被分组,并且每个分组独立地进行卷积操作(标准卷积相当于只有一个分组,所有通道之间信息会互通)。
以G代表分组数,分组卷积的计算消耗是$H\times W\times N\times K\times K\times M/G$,其计算消耗只有标准卷积的$\frac{1}{G}$。下图是一个示例,$3\times3$卷积,分组$G=2$。我们可以看到通道域的连接数变小了,也就是计算消耗变小。

进一步,分组数变为$G=3$时的连接示意图,更加稀疏。

卷积$1\times1$分组数为$G=2$时的示意图如下,卷积$1\times 1$也可以被分组,即ShuffleNet所使用的卷积。

进一步的,分组变成$G=3$时的示例

1.4 depthwise卷积
depthwise卷积其实是在输入通道上独立地做卷积操作,也可以认为是分组卷积的一种极端情况,即输入输出通道数目相同,分组G等于通道数

depthwise卷积通过略去通道域上的卷积极大的减小了计算消耗。
1.5 通道混排
通道混排是一个改变了通道的顺序操作(层),被用在ShuffleNet中。可以使用tensor reshape和transpose操作实现。
假设$GN’(=N)$表示输入通道数目,输入通道维度首先reshape成$(G,N’)$,然后将$(G,N’)$转置(transpose)到$(N’,G)$最终faltten到与输入维度一致。此处G代表了分组卷积的分组数,它同样被用到ShuffleNet中。
通道混排的计算消耗无法用乘-加(multiply-add)操作来定义。如下图,通道混排,分组G=2,没有执行卷积,只是改变了通道的顺序。

G=3的通道混排

2 高效网络
2.1 ResNet(Bottleneck 版本)
ResNet中的bottleneck架构的残差单元如下:
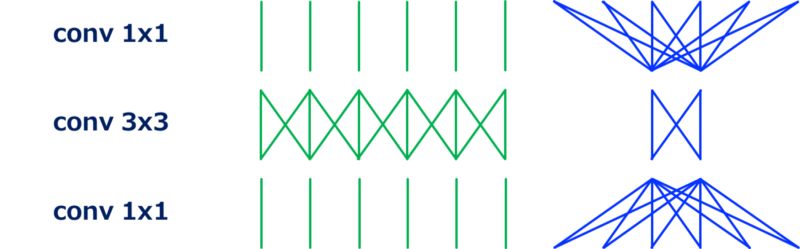
可以看到残差单元都是由 $1\times1$和$3\times3$组成的。
- 第一个$1\times1$卷积减小了输入通道的维度,减小了接下来的相对耗费计算资源的$3\times3$卷积
- 最后一个$1\times1$卷积恢复了输出通道的维度
2.2 ResNeXt
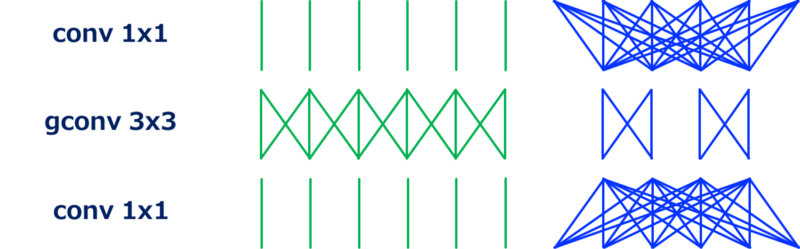
ResNeXt可以看做是ResNet的特殊版本,其$3\times3$卷积部分被替换为分组的$3\times3$卷积。使用分组卷积之后,$1\times1$所造成的通道缩减率变得比ResNet温和一些,这也导致其比ResNet在同等计算消耗情况下更好的准确率。
2.3 MobileNet(分离卷积)
MobileNet是一个分离卷积的堆,由depthwise卷积和$1\times1$卷积组成。

分离卷积在空间尺度和通道域执行卷积。卷积因子显著地将计算消耗从$H\times W\times N\times K\times K\times M$减小到$H\times W\times N\times K\times K$(depthwise)+$H\times W\times N\times M$($1\times1$卷积),即总共计算消耗为$(H\times W\times N)\times(K^2+M)$.由于$M>>K(例如 K=3并且M\ge 32)$,计算量缩减到1/8至1/9.
最重要的点,此时的计算瓶颈在$1\times1$卷积。
2.4 ShuffleNet
ShuffleNet的动机是上面提到的计算瓶颈变成了$1\times1$卷积。但是$1\times1$卷积已经高效了,似乎已经没有优化空间,但是此时可以用分组的$1\times1$卷积。
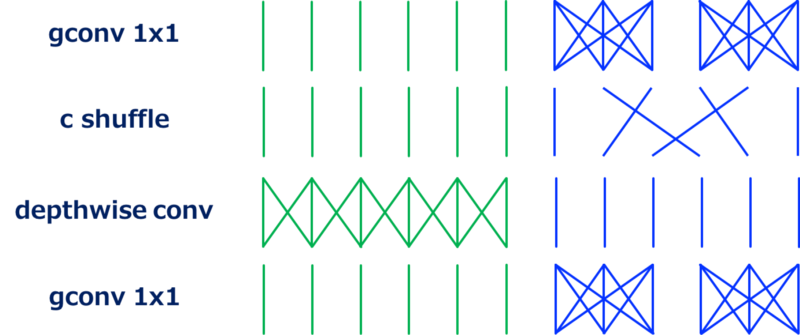
上图展示了ShuffleNet的模块,此处的重要block是通道混排层,它会混排分组卷积的不同组之间的通道顺序。如果没有通道混排,分组卷积之间的输出都不会发生联系,这会导致准确率的衰弱。
2.5 MobileNetv2
MobileNetv2使用了一个类似ResNet的残差单元的网络架构,修改版本的残差单元中$3\times3$卷积被depthwise卷积替代。
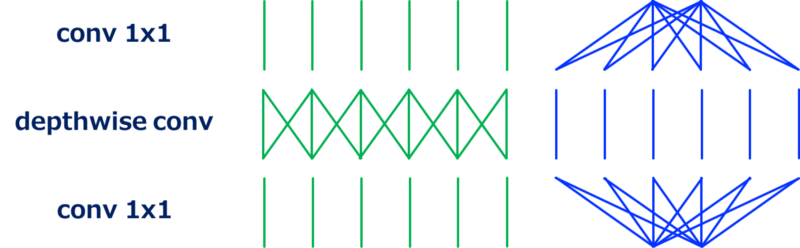
从上图可以看到,与标准bottleneck架构相比,第一个$1\times1$卷积增加了通道维度,然后执行depthwise卷积,最后再减少通道维度。通过如下图这样重排building block,我们可以看到这个架构是如何起作用的(此重排序过程没有改变网络架构,因为mobilenetv2架构就是此模块的堆叠)。
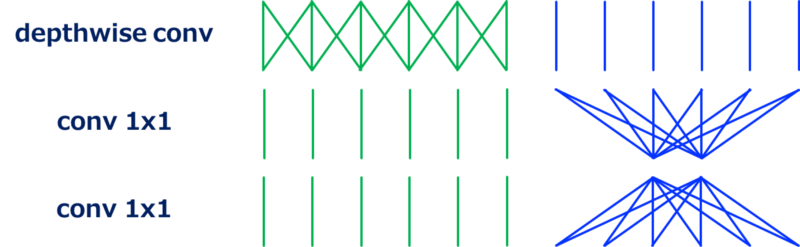
也即此模块被当做修改版本的分离卷积,其中的分离卷积中的单个$1\times1$卷积被扩充到2个$1\times1$卷积。将T作为通道方向上的扩充因子,两个$1\times1$卷积的计算消耗是 $2\times W\times H\times N^2/T$,而分离卷积中的$1\times1$卷积的计算消耗是$H\times W\times T^2$
2.6 FD-Mobilenet
Fast-Downsampling MobileNet (FD-MobileNet),此网络架构与MobileNet相比其下采样在网络的更早的层就开始了,这个简单的trick可以减小计算消耗。原因在于传统的下采样策略和可分离卷积的计算消耗。
从VGGnet开始大部分的网络都 采取相同的下采样策略:执行下采样然后在接下来的网络层将通道数翻倍。对于标准卷积,其计算消耗并没有并没有在下采样之后减小,因为是由公式$H\times W\times N\times K^2\times M$定义的。然而,对于分离卷积,其计算消耗在下采样之后变小了,从$H\times W\times N\times(K^2+M)$到$H/2\times W/2\times 2\times N\times(K^2+2M)=H\times W\times N(K^2/2+M)$。当M不是很大(比如网络的前面的层)时是有一些比较优势的。