0 定义
问题:假设要进行人脸识别,但是人脸与摄像头之间距离忽远忽近,单一分辨率的识别算法无法识别所有距离下的人脸特征。
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。
把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
示例图形金字塔

获取金字塔步骤
- 利用低通滤波器平滑图像
- 对平滑图像进行采样。有两种采样方式:
上采样(分辨率逐渐升高),下采样(分辨率直接按降低)
图像金字塔层数与图像大小关系
以$512\times512$为例
| 金字塔层数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 图像大小 | 512 | 216 | 128 | 64 | 16 | 8 | 4 | 2 | 1 |
尺寸变化时不够除的会进行四舍五入。
上采样和下采样
- 上采样:如果想放大图像,则需要通过向上取样操作得到,具体做法如下
- 将图像在每个方向扩大为原来的俩倍,新增的行和列以0填充
- 使用先前同样的内核(乘以4)与放大后的图像卷积,获得新增像素的近似值
在opencv中的代码很简单
1 | src = cv.pyrUp(src, dstsize=(2 * cols, 2 * rows)) |
- 下采样:为了获取层级为 $G_i+1$ 的金字塔图像,我们采用如下方法:
- 对图像G_i进行高斯内核卷积
- 将所有偶数行和列去除
在opencv中的代码
1 | src = cv.pyrDown(src, dstsize=(cols / 2, rows / 2)) |
显而易见,结果图像只有原图的四分之一。通过对输入图像$G_i$(原始图像)不停迭代以上步骤就会得到整个金字塔。同时我们也可以看到,向下取样会逐渐丢失图像的信息。 以上就是对图像的向下取样操作,即缩小图像
两种图像金字塔
- 高斯金字塔
- Laplace金字塔
2 SIFT中的高斯金字塔
高斯金字塔不是一个金字塔,而是很多组(Octave)金字塔,而且每组金字塔包含若干层。在opencv官方文档中的高斯金字塔看起来只是一上下采样,而且每一组只有一层。
构建过程
- 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
$$
G(x,y)=\frac{1}{2\pi \sigma ^2}e^{-\frac{(x-x_0)^2+(y-y_0)^2}{2\sigma ^2}}
$$
对于参数σ,在Sift算子中取的是固定值1.6。
将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:$0,σ,kσ,k^2σ,k^3σ……k^{L-2}σ$。
将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:$0,σ,kσ,k^2σ,k^3σ……k^{(L-2)}σ$。但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔,结构如下:
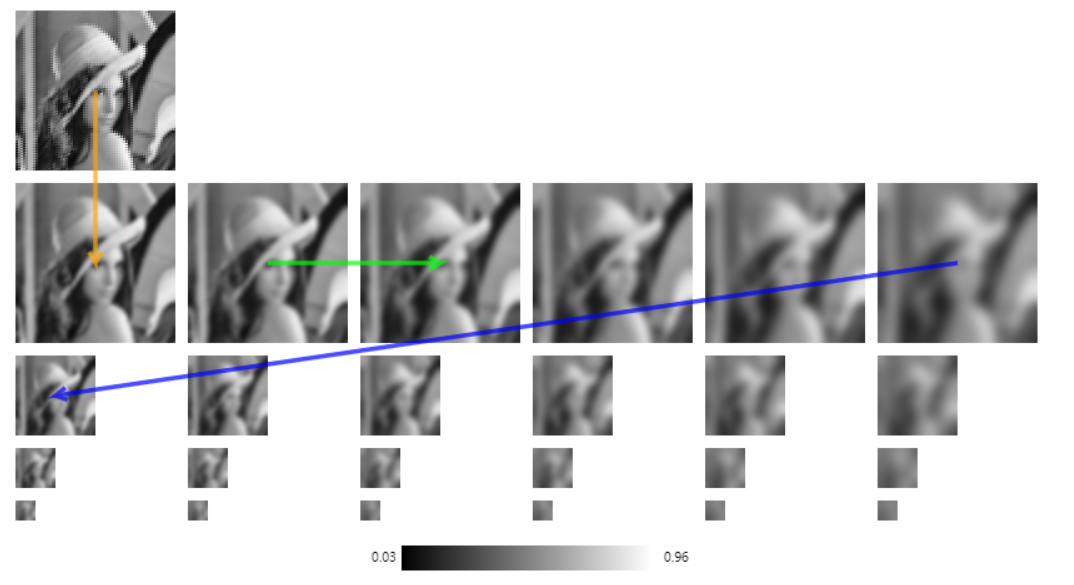
上图第一行的单独一副图像是原图经过了双线性插值做了上采样使得图像尺寸扩充了4倍(高度和宽度各扩充一倍)。图像一共4行6列,代表了图像金字塔有4层,6组(也称之为八度)。同一列,从上至下是降采样过程,可以看到图像尺寸不断缩小;同一行,从左往右是使用不同平滑系数进行高斯模糊过程,可以看到图像越来越模糊。【注意此图是灰度图演示过程,下面的图是在原图基础上做的,所以效果不一样】
代码示例
我们以下图的lnea.jpg为例
得到的图像金字塔结果如下
代码位于 python实现图像金字塔
3 差分金字塔DOG
DOG(差分金字塔)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG差分金字塔。
构建过程
差分金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。
概括为差分金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。图示如下
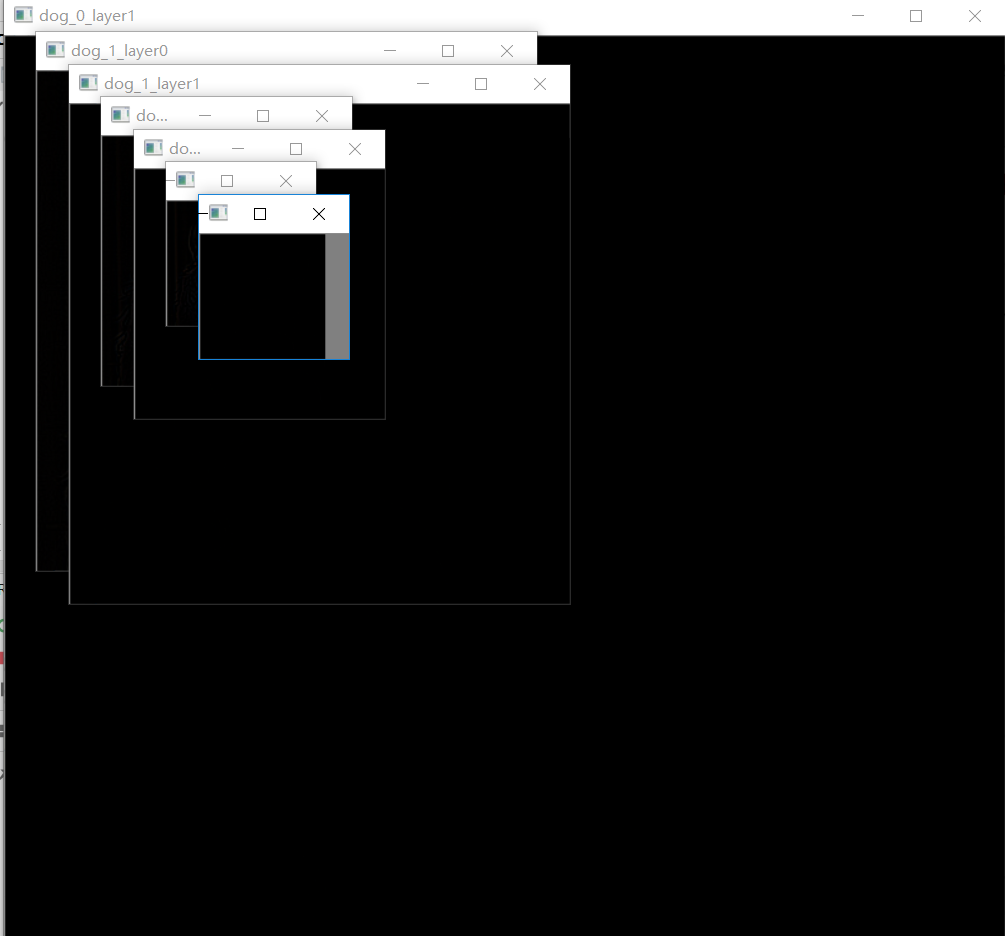
可以看到结果都是黑的,人眼看不到效果。实际计算结果包含了大量信息点。
我们对结果进行归一化操作,此时就变成了laplace金字塔了。
4 laplace金字塔
之前一直没弄清楚,差分金字塔和laplace金字塔之间的关系。直到看到这个文档
我们先看差分金字塔的公式定义:
$$
Dog(x,y,\sigma)=(G(x,y,k\sigma)-G(x,y,\sigma))*I(x,y) =L(x,y,k\sigma)-L(x,y,\sigma) \
其中 G(x,y,\sigma)代表了高斯核,G(x,y,\sigma)=\frac{1}{\sqrt{2\pi}}e^{\frac{x^2+y^2}{2\sigma ^2}},而L(x,y,\sigma)=G(x,y,\sigma)*I(x,y)
$$
缩放之后的LoG表达式为:
$$
LoG(x,y,\sigma)=\sigma ^2\bigtriangledown ^2 L(x,y,\sigma) \
= \sigma ^2(L_{xx}+L_{yy})
$$
最终推导结果如下:
$$
(k-1)\sigma ^2LoG \approx =DoG
$$
可以看到,DoG近似等于将LoG尺度缩放到一个常量$k-1$.
我们来看实际效果,借助opencv的api
1 | cv2.normalize(im, None, alpha=0, beta=1, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_32F) |
得到结果如下,可以看到清晰地特征。
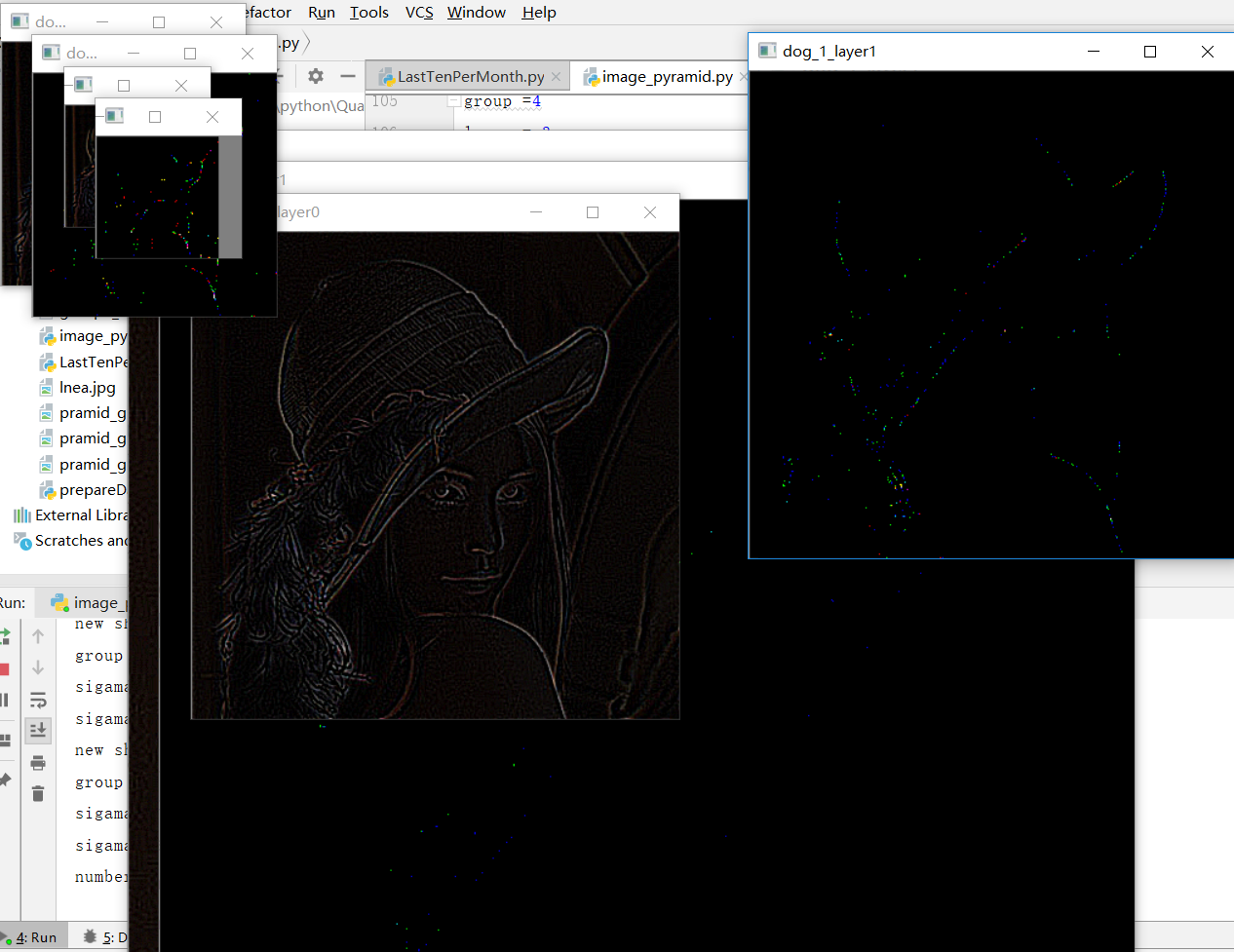
代码位于 python实现图像金字塔
此特征可以等价理解成Laplace特征。
参考