1 Haar特征
Haar特征最早是由应用于人脸特征表示时提出的,此特征反映的是图像部分区域内灰度变化情况,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。
Haar特征有4类: 边缘特征,线性特征,中心特征,对角线特征,如下图示例,这些,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。
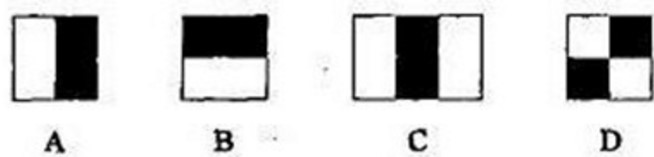
如何计算上面特征
- 对于A和B :$特征值=sum _白-sum_黑$
- 对于C:$特征值=sum _白-2\times sum_黑$,白色乘以2的原因是,保持与黑色区域一样的像素数目。
通过改变特征模板的大小和位置,可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”。而特征类别、大小和位置的变化,使得很小的检测窗口含有非常多的矩形特征。这就带来了两个问题
- 如何快速计算那么多的特征: 积分图
- 哪些矩形特征才是对分类器分类最有效的:训练分类算法,如AdaBoost
2 积分图
积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法。核心思想是:将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中,当要计算某个区域的像素和时可以直接索引数组的元素,不用重新计算这个区域的像素和,从而加快了计算。
积分图是一种能够描述全局信息的矩阵表示方法。积分图的构造方式是位置(i,j)处的值ii(i,j)是原图像(i,j)左上角方向所有像素的和。
积分图的构建算法
- 用$s(i,j)$表示行方向的累加和,初始化$s(i,-1)=0$
- 用$ii(i,j)$表示一个积分图像,初始化$ii(-1,i)=0$
- 逐行扫描图像,递归计算每个像素$(i,j)$行方向的累加和$s(i,j)$和积分图像$ii(i,j)$的值。
$$
s(i,j)=s(i,j-1)+f(i,j) \
ii(i,j)=ii(i-1,j)+s(i,j)
$$ - 扫描图像一遍,当到达图像右下角像素时,积分图像ii就构造好了。
计算方块内的像素和
计算好了积分图,我们接下来就可以利用积分图来加速计算某个方块内部的像素的和
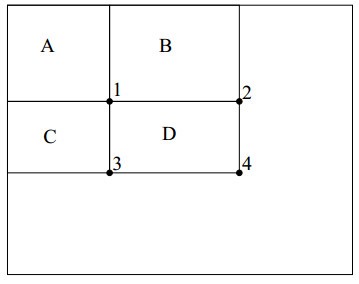
如上图,假设我们想计算区域D的像素和。上图中D的四个顶点分别是1,2,3,4。令$rectsum_n$代表顶点$n$左上角的所有像素和,那么区域D内的像素和为: $rectsum_4-rectsum_2-rectsum_3+rectsum_1,注意顶点1的坐上所有像素和被减了2次,所以要加一次$
3 Adaboost 算法
opencv中关于adaboost训练过程参考 opencv tutorial_traincascade
后面再讲到 Adaboost算法时,再详细说明。
4 opencv 中使用haar特征检测人脸
opencv已经预先包含了多种训练好的人脸分类器,眼睛分类器,微笑分类器等。可以自己定义和训练一个,此处直接使用opencv已经训练好的人脸级联分类器,它的算法原理就是使用了Haar特征+Adaboost算法训练出的级联分类器。
首先,载入xml定义的分类器,载入的图像必须是灰度图
1 | import numpy as np |
接着开始检测人脸,如果有检测到则画出矩形框,下图是检测结果(同时包含了眼睛检测)
1 | faces = face_cascade.detectMultiScale(gray, 1.3, 5) |

5 Haar特征拓展
5.1 ABH特征
为提高二分Haar特征的区分能力,我们提出 了一种多二分Haar特征,并使用它们的共现性作为新的特征,成为ABH(Asseming Binary Haar)特征。
下图演示了ABH特征的一个例子。
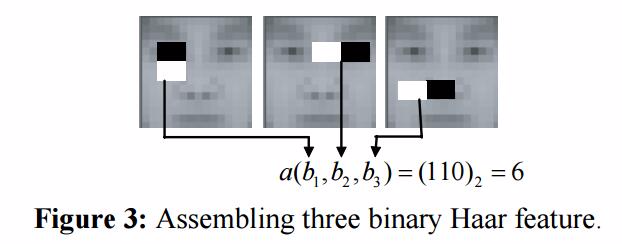
上图中ABH特征集成了三个二分Haar特征,当三个二分Haar特征值分别为1,1,0时,ABH特征为 a(b1,b2,b3)=(110)2=6
其中 a为三个二分Haar特征 b1,b2,b3 的ABH特征计算函数, (.)2 是一个从二进制转十进制的操作。特征值说明了对 2F个不同结合的index,其中F是结合的二分特征数。
5.2 LAB(Locally Assembing Binary)特征
ABH特征的数目巨大。为了枚举所有的特征,需要几个自由参数,比如二分Haar特征的集合数目,每个二分Haar特征的大小,每个二分Haar特征的坐标位置。从如此巨大的特征池中学习是不可逆的。我们发现了一种对应的用于人脸检测的缩减集合,称为LAB Haar特征。
ABH特征之中,LAB特征是那些结合8个局部邻接2-矩形的二分Haar特征,它们大小相同并且共享同一个中心矩形。下图展示了一个8个二分Haar特征用以集合为一个LAB特征。
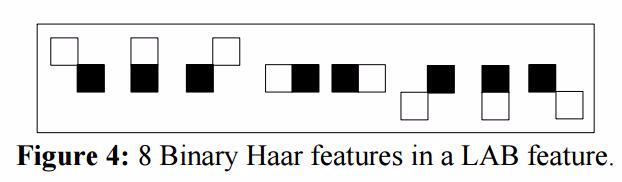
下图是一个2个LAB特征的示例
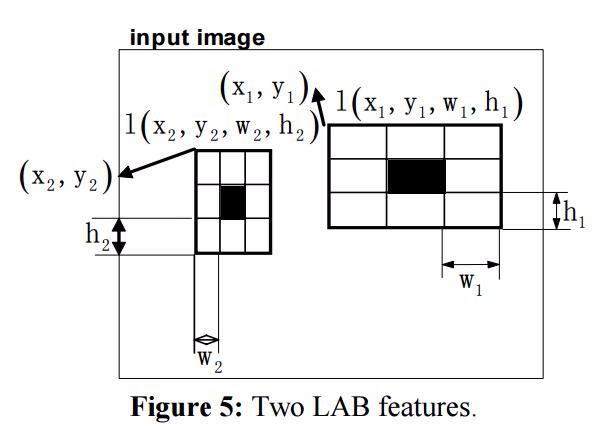
图中展示了两个不同的LAB特征,中心的黑色矩形被8个相邻的二分Haar特征共享,所有9个矩形都是相同的大小。
从公式上看,一个LAB特征可以用一个四元组表示 l(x,y,w,h) ,其中 x,y 分别代表了左上角的x和y轴坐标,(w,h) 代表了矩形的宽和高。
LAB特征保留了所有二分Haar特征的优势,同时又很强的区分能力,大小也很小。LAB特征抓取了图像的局部强度。计算LAB特征需要计算8个2-矩形Haar特征。LAB特征值区间为 {0,…255},每个值对应了特别的局部结构。