HOG特征详解

0 简介

HOG特征即 Histogram of oriented gradients，源于2005年一篇CVPR论文，使用HOG+SVM做行人检测，由于效果良好而被广泛应用。大体效果如下，具体使用HOG+SVM做行人检测时再讨论详细代码。

算法计算步骤概览

图像预处理。伽马矫正(减少光度影响)和灰度化(也可以在RGB图上做，只不过对三通道颜色值计算，取梯度值最大的)【可选步骤】
计算图像像素点梯度值，得到梯度图(尺寸和原图同等大小)
图像划分多个cell，统计cell内梯度直方向方图
将$2\times 2$个cell联合成一个block,对每个block做块内梯度归一化

1 图像预处理

1.1 gamma矫正和灰度化

作用：gamma矫正通常用于电视和监视器系统中重现摄像机拍摄的画面．在图像处理中也可用于调节图像的对比度，减少图像的光照不均和局部阴影．
原理：通过非线性变换，让图像从暴光强度的线性响应变得更接近人眼感受的响应，即将漂白（相机曝光）或过暗（曝光不足）的图片，进行矫正

gamma矫正公式：
$$
f(x) =x^{\gamma}
$$
即输出是输入的幂函数，指数为$\gamma$

代码实现如下

import cv2
import numpy as np

img = cv2.imread('gamma0.jpg',0)
img1 = np.power(img/float(np.max(img)), 1/1.5)
img2 = np.power(img/float(np.max(img)), 1.5)

cv2.imshow('src',img)
cv2.imshow('gamma=1/1.5',img1)
cv2.imshow('gamma=1.5',img2)
cv2.waitKey(0)

下图分别代表了处理之后的原图,灰度图，gamma=1/1.5矫正,gamma=1.5矫正

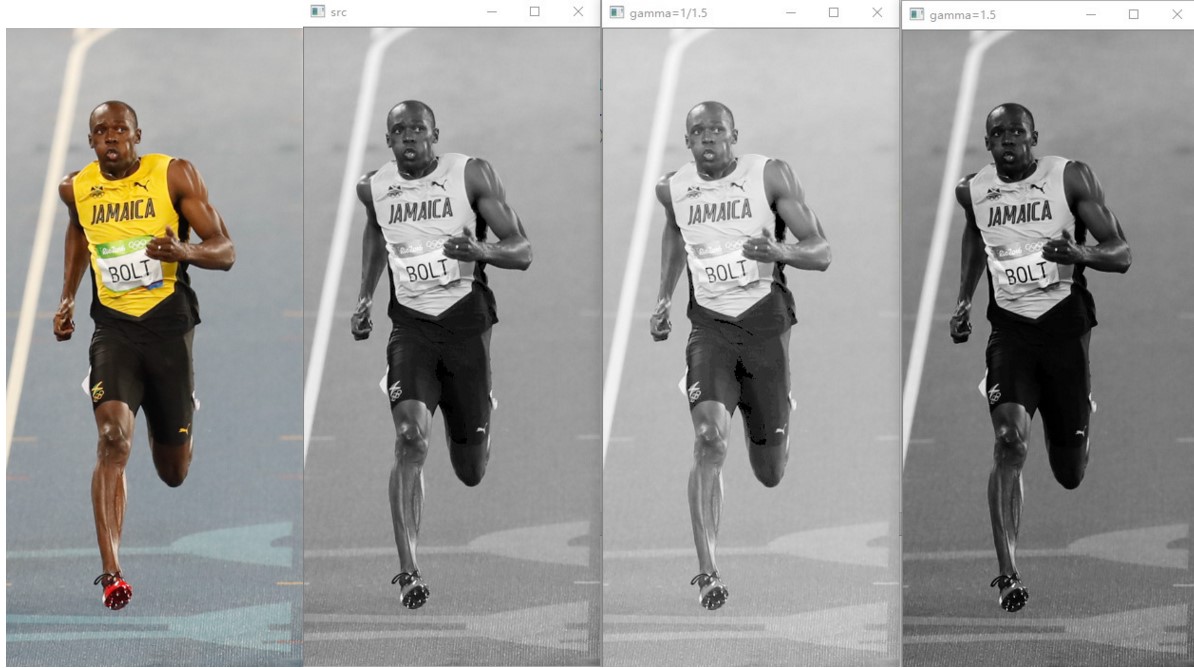
2 计算图像像素梯度图

我们需要同时计算图像的水平梯度图和垂直梯度图 。如下图，假设我们要计算下图中像素点A的梯度值，

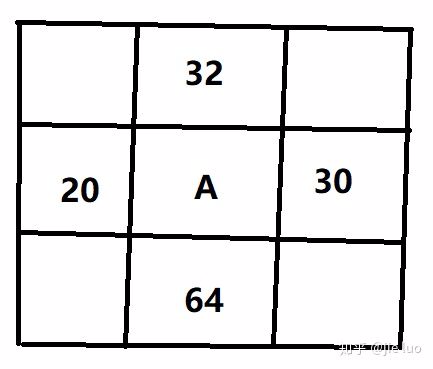
计算方法为

梯度大小

水平梯度： $g_x=\sqrt {(L(x-1,y)-L(x+1,y))^2}=\sqrt{(30-20)^2}=\sqrt{10^2}=10$
垂直梯度： $g_y=\sqrt {(L(,y+1)-L(x,y-1))^2}=\sqrt{(32-64)^2}=\sqrt{32^2}=32$

梯度方向

+
$$
\theta (x,y) = arctan [\frac{g_x}{g_y}] =arctan\frac{10}{32}
$$

梯度方向会取绝对值，因此得到的角度范围是 $[0,180°]$

上面这些计算过程，在opencv中有对应的算子，称为Sobel算子，分别计算水平和垂直方向梯度的。

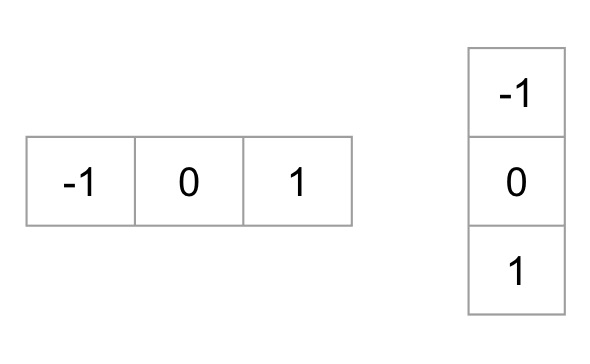
使用的python opencv代码为

im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0
 
# 计算梯度
img = cv2.G
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
# 计算梯度幅度和方向
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
cv2.imshow("absolute x-gradient",gx)
cv2.imshow("absolute y-gradient",gy)
cv2.imshow("gradient magnitude",mag)
cv2.imshow("gradient direction",angle)
cv2.waitKey(0)

效果如下，分别为原图,x方向梯度绝对值,y方向梯度绝对值图,梯度幅度图,梯度方向图
下图是没有使用归一化效果

使用归一化之后的效果

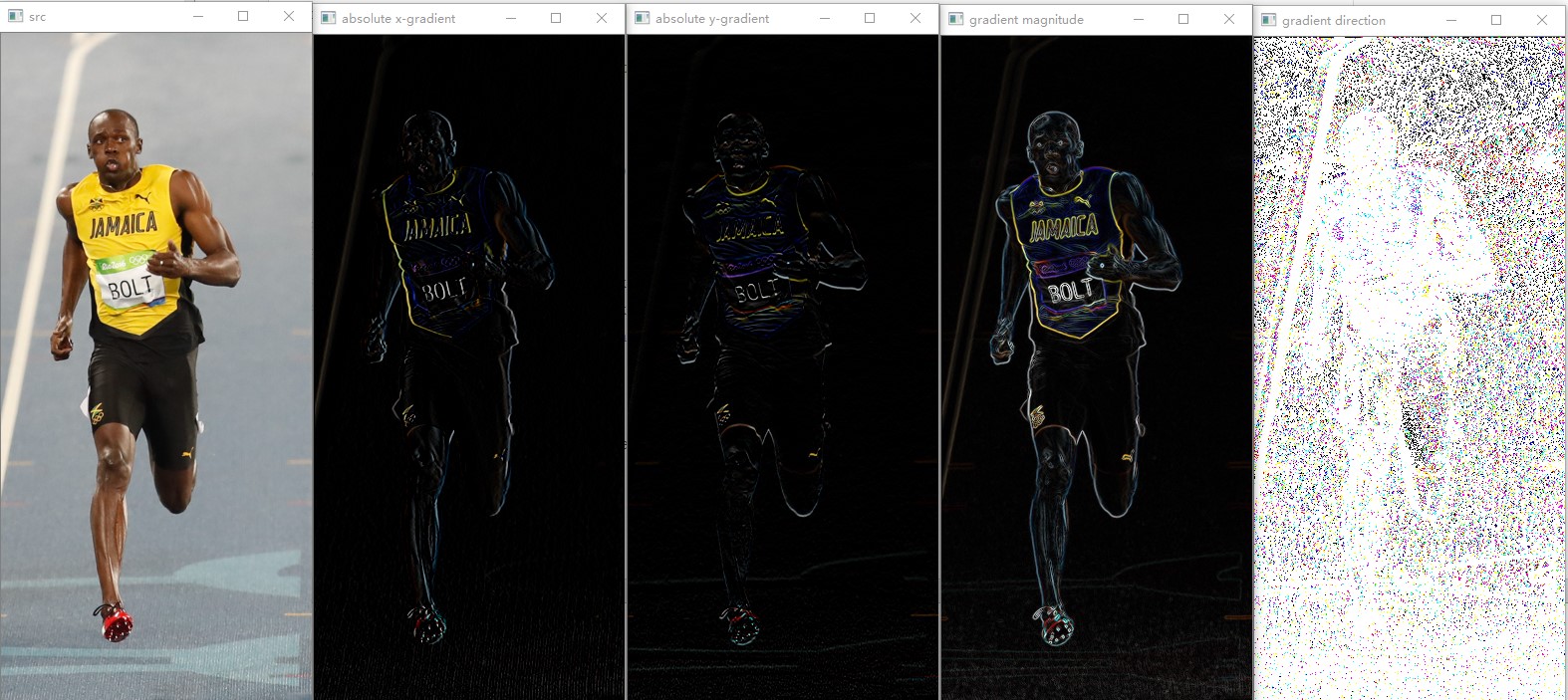
可以看到

x方向梯度图会强化垂直方向的特征，可以观察到左侧白色斜线更加明显，但是底部一些水平线没有了。
y方向梯度图会强化水平方向特征，底部水平线强化了，左侧垂直线不是那么明显了。

梯度图移除了大量非显著性特征，并加强了显著特征。三通道的彩色图中，每个像素的梯度幅度是三个通道中最大的那个，而梯度方向是梯度幅度最大的那个通道上的方向。

3 计算梯度直方图

经过上一步计算之后，每个像素点都会有两个值：梯度方向和梯度幅度。

但是，也看到了，梯度幅度和梯度方向图与原图等同大小，实际如果使用这些特征，会存在两个问题

计算量很大，基本就是原图
特征稀疏。图中其实只有少量稀疏的显著特征，大部分可能是0

以上是个人理解。

HOG特征在此步骤选择联合一个$8\times 8$的小格子内部一些像素，计算其梯度幅度和梯度方向的统计直方图，这样一来就可以以这个梯度直方图来代替原本庞大的矩阵。每个像素有一个梯度幅度和梯度方向两个取值，那么一个$8\times 8$的小格子一共有$8\times 8\times 2=128$个取值。

上面提到，梯度方向取值范围是$[0,180]$，以每20°为一个单元，所有的梯度方向可以划分为9组，这就是统计直方图的分组数目。如下图，我们选取划分格子之后的第二行第二列一个小单元，计算得到右边的梯度方向图和梯度幅度图，同时以以梯度方向为index，统计分组数量。

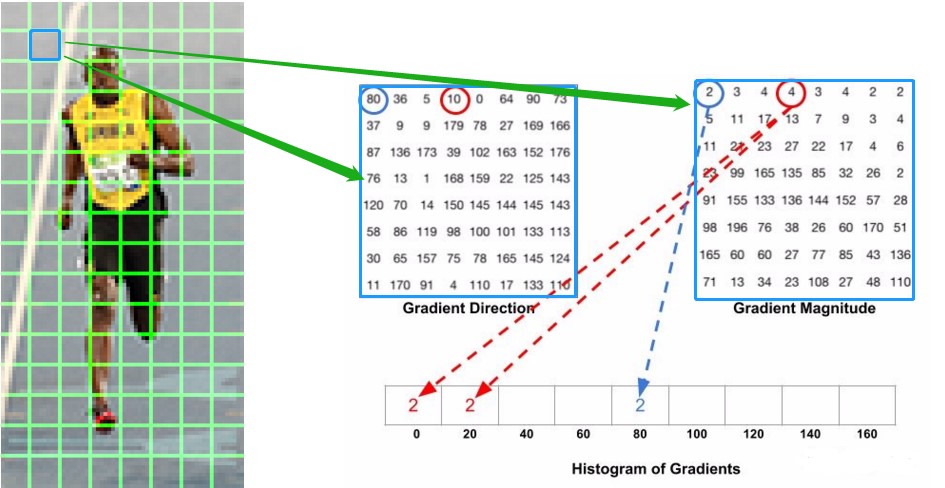
得到的统计频率直方图如下

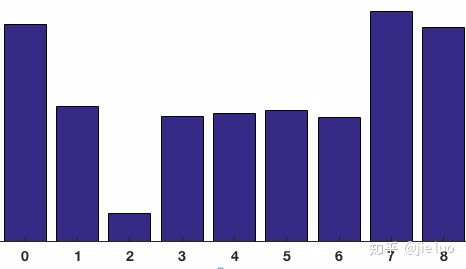
从上图可以看到，更多的点的梯度方向是倾向于0度和160度，也就是说这些点的梯度方向是向上或者向下，表明图像这个位置存在比较明显的横向边缘。因此HOG是对边角敏感的，由于这样的统计方法，也是对部分像素值变化不敏感的，所以能够适应不同的环境。

至于为什么选取$8\times 8$为一个单元格，是因为HOG特征当初设计时是用来做行人检测的。在行人图片中$8\times8$的矩阵被缩放成$64\times 128$的网格时，足以捕获一些特征，比如脸部或者头部特征等。

4 block归一化

目的：降低光照的影响
方法：向量的每一个值除以向量的模长

比如对于一个$(128,64,32)$的三维向量来说，模长是$ \sqrt{128^2+64^2+32^2}=146.64$,那么归一化后的向量变成了$(0.87,0.43,0.22)$。

HOG在选取$8\times 8$为一个单元格的基础之上，再以$2\times 2$个单元格为一组，称为block。作者提出要对block进行归一化，由于每个单元格cell有9个向量，$2\times 2$个单元格则有36个向量，需要对这36个向量进行归一化。下图演示了如何在图像中抽取block

5 HOG特征描述

每一个$16\times 16$大小的block将会得到36大小的vector。那么对于一个$64\times128$大小的图像，按照上图的方式提取block，将会有7个水平位置和15个竖直位可以取得，所以一共有$7\times15=105$个block，所以我们整合所有block的vector，形成一个大的一维vector的大小将会是$36\times105=3780$。

6 参考代码

计算图像HOG特征时，我们使用如下代码

import matplotlib.pyplot as plt
from skimage.feature import hog
from skimage import data, exposure
image = cv2.imread('C:/Users/dell/Desktop/123.png')

fd, hog_image = hog(image, orientations=8, pixels_per_cell=(16, 16),
                    cells_per_block=(1, 1), visualize=True, multichannel=True)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4), sharex=True, sharey=True)
ax1.axis('off')
ax1.imshow(image, cmap=plt.cm.gray)
ax1.set_title('Input image')
# Rescale histogram for better display
hog_image_rescaled = exposure.rescale_intensity(hog_image, in_range=(0, 10))
ax2.axis('off')
ax2.imshow(hog_image_rescaled, cmap=plt.cm.gray)
ax2.set_title('Histogram of Oriented Gradients')
plt.show()

效果如下

7 参考

知乎图像HOG特征计算
 图像gamma矫正
 梯度计算
 skimage 计算图像HOG特征