重新出发

0%

SIFT特征详解

发表于 分类于
图像特征

1 概览

SIFT特征即Scale-Invariant Feature Transform，是一种用于检测和描述数字图像中的局部特征的算法。它定位关键点并以量化信息呈现（所以称之为描述器），可以用来做目标检测。此特征可以被认为可以对抗不同变换（即同一个特征在不同变换下可能看起来不同）而保持不变。

可以通过这个网站 SIFT特征在线计算，直接查看一张图片中的SIFT特征，你需要准备一张小图片，然后上传到网站，就会自动计算出该图像的SITF特征。如果对SIFT特征计算步骤缺乏形象的认识，可以去这个网站互动下，它可以可视化每个步骤。

SIFT特征的提取步骤

  1. 生成高斯差分金字塔（DOG金字塔），尺度空间构建
  2. 空间极值点检测（关键点的初步查探）
  3. 稳定关键点的精确定位
  4. 稳定关键点方向信息分配
  5. 关键点描述
  6. 特征点匹配

2 生成差分高斯金字塔

参考 图像处理中各种金字塔 得到一组如下图

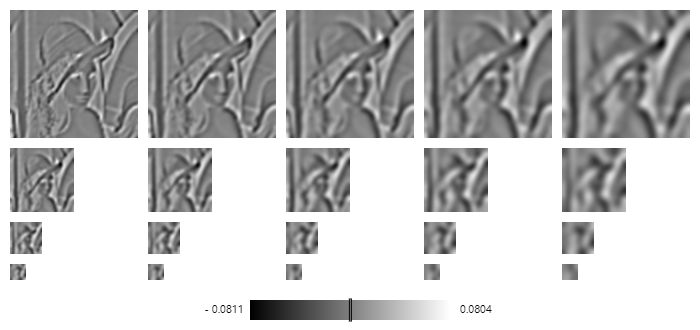
sift1

3 空间极值点检测

从第2步的差分高斯金字塔(DOG)中可以得到不同层级不同尺度的金字塔，所谓的特征就是一些强的、有区分力的点。DOG中这些有区分力的点就是极值点，即每个像素都要和相邻点(此处的相邻不仅仅是水平面的前后左右，还有上下尺度的前后左右)比较，看其是否比它的图像域(水平方向上)和尺度空间域(垂直方向上)的相邻点大或者小，下图是示意图：

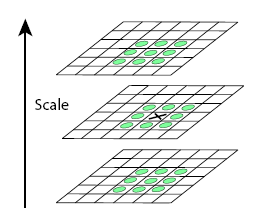
sift1

在二维图像空间，中心点与它33邻域内的8个点做比较，在同一组内的尺度空间上，中心点和上下相邻的两层图像的29个点作比较，如此可以保证检测到的关键点在尺度空间和二维图像空间上都是局部极值点。所以确定极值点，需要$3\times 3-1(当前像素点，上图中中间黑色X)+2\times 9=26个点$。
从第2小节中，我们计算得到的极值点由如下黄色和红色标记（其中黄色圆圈的标记表明，它虽然是极值点，但是由于绝对值过小，在后续处理时会被丢弃）

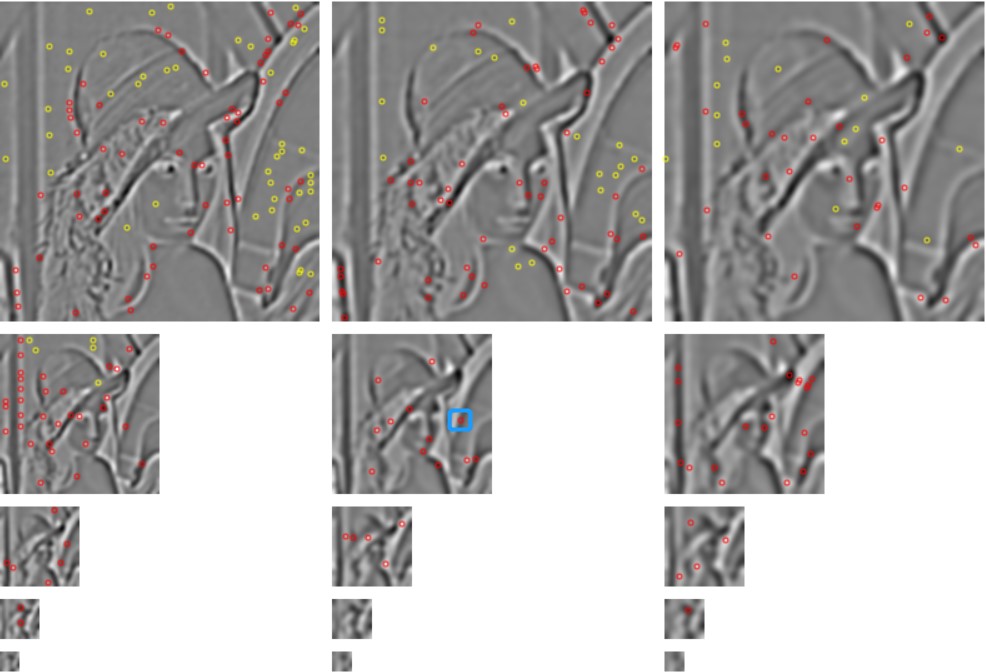
sift1

我们选取图中间用蓝色矩形框标记的红色点，查看其灰度值(下图正中间红色点)，可以看到它在当前差分金字塔取得了极小值。

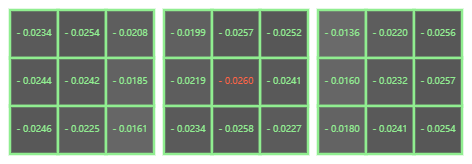
sift1

4 稳定关键点的精确定位

上面步骤得到的极值点中存在大量不稳定地点，有些可能是噪音导致的，比如第3节中黄色圆圈标记的点。我们需要去除这些不稳定地像素点。即去除DOG局部曲率非常不对称的像素。此步骤，需要计算空间尺度函数的二次泰勒展开式的极值来完成。同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

具体步骤如下：

  1. 空间尺度函数泰勒展开式如下：
    $$
    D(x)=D+\frac{\partial D^T}{\partial x}x+\frac{1}{2}x^T\frac{\partial ^2D}{\partial x^2}x \
    对上式求导，令其为0，得到精确地位置，有\
    \hat x=-\frac{\partial ^2D^{-1}}{\partial x^2}\frac{\partial D}{\partial x}
    $$

  2. 在已经检测到的特征点中，要去掉低对比度的特征点和不稳定地边缘响应点。去除低对比度的点：把$\hat x$的值代回，即在Dog 空间的极值点$D(x)$处取值，只取前两项可得：
    $$
    D(\hat x)=D+\frac{1}{2}\frac{\partial D^T}{\partial x}\hat x
    $$
    若 $|D(\hat x)\ge 0.003$，该特征点就保留下来，否则丢弃

3.边缘响应的去除。一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的曲率，而在垂直边缘的方向有较小的曲率。主曲率通过一个$2\times 2$的Hessian矩阵H去求出：
$$
H=[ \begin{array} D_{xx} \quad D_{xy} & \
D_{xy}\quad D_{yy} &
\end{array} ]
$$
使用python计算hessian矩阵的代码可以参考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np

def hessian(x):
    """
    Calculate the hessian matrix with finite differences
    Parameters:
       - x : ndarray
    Returns:
       an array of shape (x.dim, x.ndim) + x.shape
       where the array[i, j, ...] corresponds to the second derivative x_ij
    """
    x_grad = np.gradient(x) 
    hessian = np.empty((x.ndim, x.ndim) + x.shape, dtype=x.dtype) 
    for k, grad_k in enumerate(x_grad):
        # 遍历每个维度，在一阶导数的所有项再次使用梯度
        tmp_grad = np.gradient(grad_k) 
        for l, grad_kl in enumerate(tmp_grad):
            hessian[k, l, :, :] = grad_kl
    return hessian

x = np.random.randn(100, 100, 100)
hessian(x)

导数由采样点相邻差估计得到。D的主曲率和H的特征值成正比，令α为较大特征值，β为较小的特征值，则
$$
Tr(H)=D_{xx}+D_{yy}=\alpha +\beta \
Det(H)=D_{xx}D_{yy}-(D_{xy})^2 = \alpha\beta \
令\alpha=\gamma \beta则 \
\frac{Tr(H)^2}{Det(H)} =\frac{(\alpha+\beta)^2}{\alpha \beta}=\frac{(\gamma\beta +\beta)^2}{\gamma \beta ^2}=\frac{(1+\gamma)^2}{\gamma}
$$
而$\frac{(1+\gamma)^2}{\gamma}$的值在两个特征值相等的时候最小，随着$\gamma$的增大而增大，因此，为了检测主曲率是否在某阈值$\gamma$下，只需检测
$$
\frac{Tr(H)^2}{Det(H)}<\frac{(\gamma+1)^2}{\gamma}
$$
在SIFT特征提取的原论文中，提到如果$\frac{\alpha +\beta}{\alpha \beta}>\frac{(\gamma +1)^2}{\gamma}$，则丢弃此像素点，论文中$\gamma=10$

5 给特征点赋值一个128维方向参数

经过上面的步骤，我们已经确定了一些灰度值极值点。接下来，我们需要确定这些极值点的方向。为关键点分配方向信息所要解决的问题是使得关键点对图像角度和旋转具有不变性。方向的分配是通过求每个极值点的梯度来实现的。
对于任一关键点

  • 其梯度幅值表述为：

$$
m(x,y) = \sqrt{((L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2}
$$

  • 梯度方向为：
    $$
    \theta (x,y) = tan ^{-1}[\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}]
    $$

分配给关键点的并不直接是关键点的梯度方向，而是按照一种梯度方向直方图方式给出的
计算方法

  1. 计算关键点为中心邻域内所有点的梯度方向。0-360度
  2. 每个方向10度，共36个方向。
  3. 统计累计落在每个方向点的关键点个数，依次生成梯度直方图

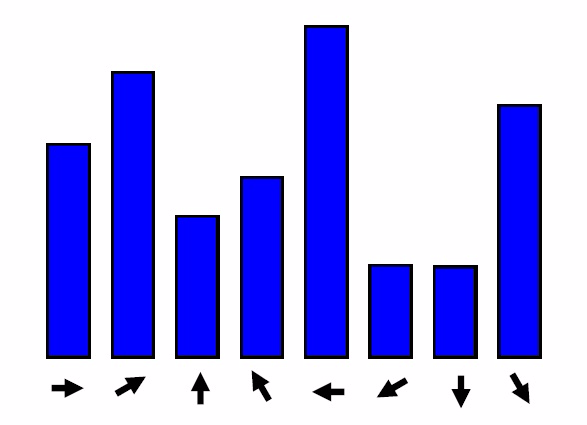
sift1

具体在图像实例中，某个极值点的梯度方向直方图如下：

sift1

上图中，左图矩形框内的红色小圆圈代表点击的极值点，中间图案代表最终得到的极值点的主方向，右图为对应的梯度方向直方图。

除此之外，原论文中还包含了辅方向，辅方向定义为：若在梯度直方图中存在一个相当于主峰值80%能量的峰值，则认为是关键点的辅方向。辅方向的设计可以增强匹配的鲁棒性，Lowe指出，大概有15%的关键点具有辅方向，而恰恰是这15%的关键点对稳定匹配起到关键作用。

6 计算SIFT特征描述子

此步骤与步骤5基本一样，也是计算每个关键点周围的梯度方向的直方图分布。不同之处在于，此时的邻居为一个圆，并且坐标体系被扭曲以匹配相关梯度方向。
具体思路是：对关键点周围像素区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象表述。
如下图，对于22块，每块的所有像素点的梯度做高斯加权，每块最终取8个方向，即可以生成228维度的向量，以这22*8维向量作为中心关键点的数学描述

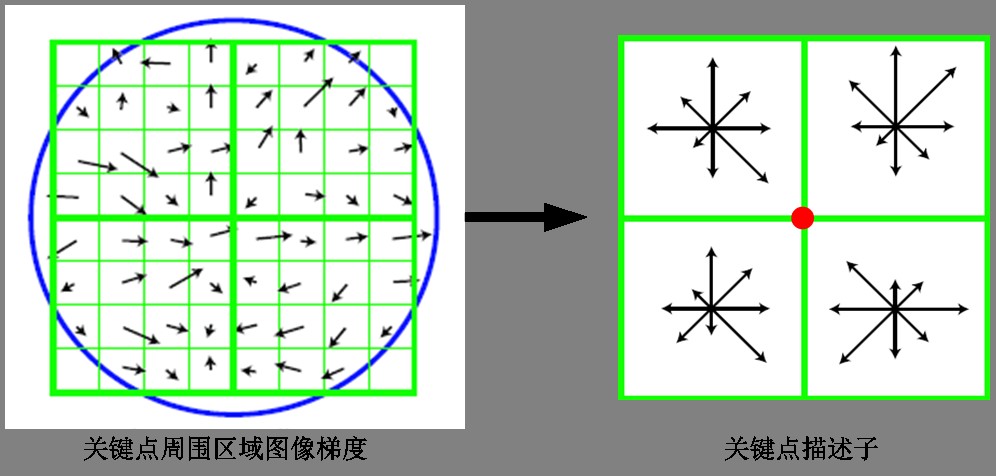
sift1

但是实际上，在原论文中证明，对每个关键点周围采用$4\times 4$块(每个块内依然是8个方向)的邻域描述子效果最佳

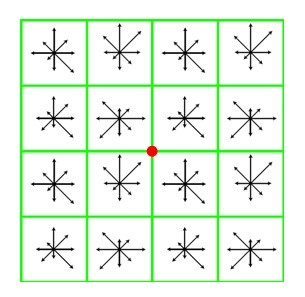
sift1

所以，此时我们计算的不是一个梯度方向直方图，而是16个。每个梯度直方图对应的是新坐标系统的中心点附近的点以及圆形周围邻居梯度的分量。

下图是某个极值点用于生成的描述子的邻居以及坐标系统，即直方图（被归一化并以$4\times 4\times 8=128$个整型数字）。仔细看下图，会发现有16个直方图(16个块)，每个直方图有8个bins(代表每个块的8个主方向)。

sift1

CSDN SIFT特征
Rachel-Zhang SIFT
stackoverflow 计算hessian矩阵