数据挖掘方法之四：多重共线性及变量选择方法

一概念

前多重共线性：也即使用的多个预测变量之间存在线性相关。多重共线性会导致解的不稳定，进而可能导致意外的结果。在线性代数中，基坐标必须是相互正交的，也即不相关的，此处在做多元回归预测时，必须保证预测变量之间是不相关的。

避免不正交的方法

1分析之前

a.逐个计算预测变量之间的相关系数

> cor(sugar$sugars,sugar$shelf)  
[1] 0.1004379  
> cor(sugar$fiber,sugar$potass)  
[1] 0.9033737

可以看到纤维和钾含量存在高度相关性，需要注意

b.为预测变量建立矩阵图

> #同时画多个变量的对照图需要使用 car包中的 scatterplotMatrix函数  
>install.packages("car")  
>library(car)  
>#使用谷物数据集的 “糖”，“纤维”，“钾”三列数据  
> sugar_frame<-as.data.frame(sugar[,c("糖","纤维","钾")])  
>#画出对照图  
> scatterplotMatrix(sugar_frame,spread=F,lty.smooth=2,var.labels=c("糖","纤维","钾"))

结果如下图：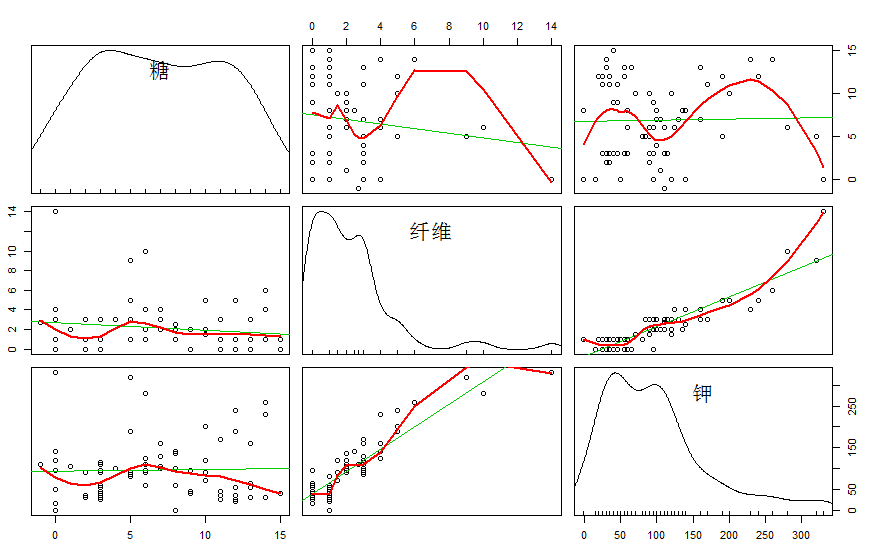

可以看到第四张和第六张是纤维和钾的相关图，可以看出他们之间有很强相关性。

1.2 分析之后：方差膨胀因子(variance inflation factors,VIFs)

$$
VIF=\frac{1}{1-R^2_i}
$$

其中 $R_i^2$ 表示 $R^2$ 的值是通过在其他预测变量上回归分析 $x_i$ 得到的。假设xi和其他变量没有任何关系,那么 $R_i^2=0$ ，于是可以得到 $VIFi=\frac{1}{1-0}=1$ 。也即VIF最小值为1，没有最大值.

$VIF_i$ 的变化对第i个系数的变化率Sbi如何产生影响，有如下公式：

$$
Sb_i=Sc_i=S\sqrt{\frac{1}{(n-1)S^2_i}\frac{1}{1-R^2_i}}=S\sqrt{\frac{VIF_i}{(n-1)S^2_i}}
$$

如果 $x_i$ 与其他预测变量不想管，那么 $VIF_i=1$ ，而且相关系数的标准差 $Sb_i$ 没有增大。然而如果xi与其他变量相关，那么较大的 $VIF_i$ 值会使得相关系数的标准差 $Sb_i$过度膨胀。因此，方差估计的膨胀会导致估计精度的下降。

粗略的经验法则如下:

VIF>=5 模型有中度的多重共线性（相当于 $R^2=0.08$ ）
VIF>=10 模型中有严重多重共线性(相当于 $R^2=0.90$ )

下面来查看谷物数据集中糖、纤维、钾的膨胀因子

> #回归拟合  
> fit<-lm(data=sugar,rating~sugars+fiber+potass)  
>#注意，我们只是用了sugar数据集中包含“糖”，“纤维”，“钾”三列数据的sugar_frame  
>#进行膨胀因子计算时，需要使用gvlma包中的vif函数，因此需要先安装  
> install.packages("gvlma")  
> library(gvlma)  
Warning message:  
程辑包‘gvlma’是用R版本3.0.2 来建造的   
>#线性模型的综合验证  
> gvlma(fit)  
  Call:  
  lm(formula = rating ~ sugars + fiber + potass, data = sugar)  

    Coefficients:  
    (Intercept)       sugars        fiber       potass    
        52.6762      -2.0510       4.3701      -0.0543    


    ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS  
    USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:  
    Level of Significance =  0.05   

    Call:  
     gvlma(x = fit)   

                         Value p-value                   Decision  
    Global Stat        7.24415 0.12353    Assumptions acceptable.  
    Skewness           5.61716 0.01779 Assumptions NOT satisfied!  
    Kurtsis           0.02125 0.88411    Assumptions acceptable.  
    Link Function      0.40164 0.52624    Assumptions acceptable.  
    Heteroscedasticity 1.20410 0.27250    Assumptions acceptable.  
    >#查看膨胀因子 vif  
    > vif(fit)  
      sugars    fiber   potass   
     1.164237 6.327286 6.204047

二. 变量选择方法

为帮助数据分析人员确定在多元回归模型中应该包含哪些变量，下面是几种变量选择方法

向前选择
向后排除
逐步选择
最优子集

注意四种选择方法所使用的数据集都是 “谷物数据集”。

2.1 向前选择程序

1.对于第一个加入模型的变量，选择与回应变量相关度最高的预测变量（假设为 $x_1$ ）如果所有变量对模型都不重要，则停止,否则执行2
2. 对其余的每个变量，F统计序列式 $F(x_2|x_1),F(x_3|x_1),F(x_4|x_1)$ .第二次通过此算法时是, $F(x_3|x_1,x_2),F(x_4|x_1,x_2)$ 。选择具有最大F统计序列的变量
3. 对 2 选择出来的变量，进行F统计序列的显著性检验。如果结果模型没有重大意义，则停止，否咋将从 2 得到的变量加入到模型中，然后返回2

初始：模型中没有变量。

结束：一次按照第二步进行，得到如下变量加入顺序：脂肪，蛋白质，碳水化合物，卡里路，维生素和钾。此时再也找不到其他显著的变量加入模型中才中断，此时的多元回归模型如下：

下图显示了一个顺序选择的模型概览: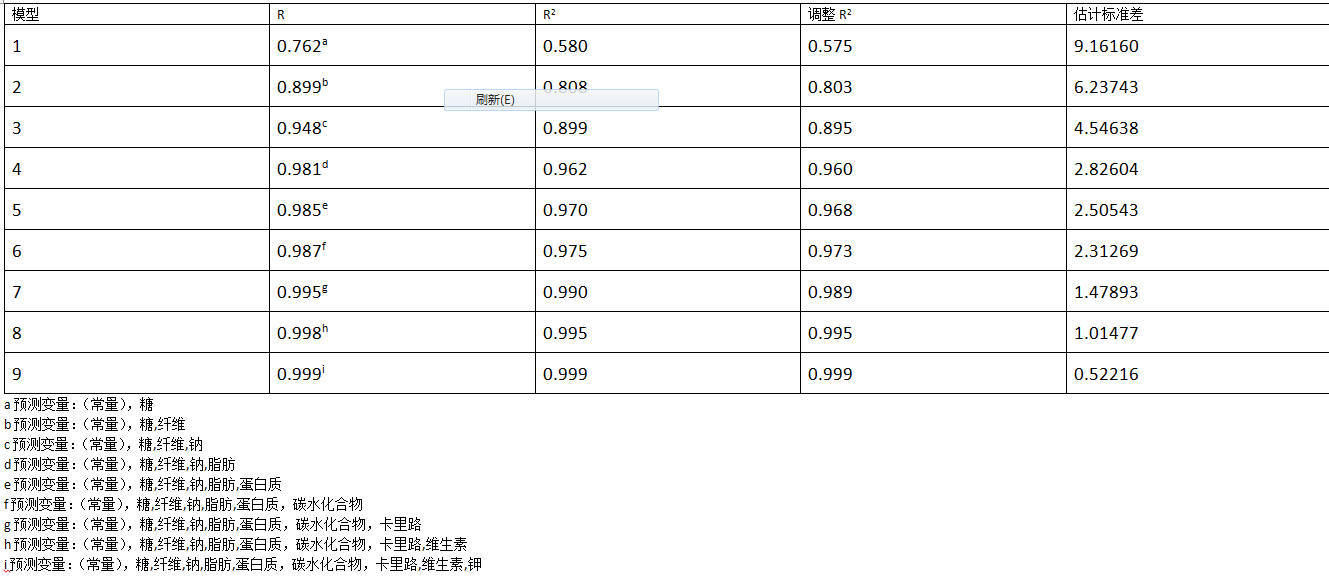

2.2 向后排除程序

向后排除程序是从模型中所有变量或者所有用户自定义变量集开始的。步骤如下:

在全模型中执行向后排除，即使用所有变量的模型。例如，可能全模型中有4个变量 $x_1,x_2,x_3,x_4$
对于当前模型中的每个变量，计算出它的偏F统计量。第一次是：$F(x_1,x_2,x_3,x_4)、F(x_2|x_1,x_3,x_4)、F(x_3|x_1,x_2,x_4)和F(x_4|x_1,x_2,x_3)$ 。选择具有最小偏F统计量的比那辆，其值用 $F_{min}$表示
检验 $F_{min}$ 的显著性。如果 $F_{min}$ 不显著，从模型中删除与Fmin对应的变量，然后返回执行2，如果 $F_{min}$ 显著，停止这个过程。

实例：
起始时模型包含了所有变量，然后计算该模型中每个变量的偏F统计量。例如，这些统计量分别是F(重量|糖，纤维，….杯子)，F(杯子|糖，纤维,…..重量|)。找到最小偏F统计量（ $F_{min}$ ）对应的变量。第一次是重量，此时 $F_{min}$ 不显著，因而从模型中去掉，接下来变量具有最小偏F统计是杯子，也是不显著的，因而需要被剔除。第三次具有最小偏F统计量的是货架2的指标变量，但是Fmin对应的p值并没有大道可以从模型中剔除，因而保留并中断。得到的模型为：

$$
y =b_0+b_1(糖)+b_2(纤维)+b_3(钠)+b_4(脂肪)+b_5(蛋白质)+b_6(碳水化合物)+b_7(卡里路)+b_8(维生素)+b_9(钾)+b_10(货架2)+e
$$

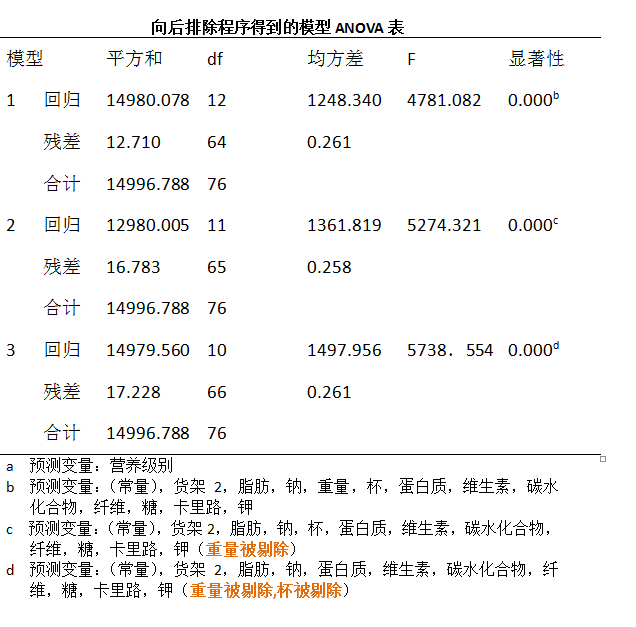模型1表示包含所有预测变量，模型2中剔除了重量之外所有预测变量，于是有：

$$
SS_{重量|所有其他变量}=SS_{所有变量}-SS_{重量以外所有变量}=12980.078-14980.005=0.073
$$

上表信息中显示，偏F统计量的结果为：

$$
F(重量|所有其他变量)= \frac{SS_{重量|所有其他变量}}{MSE_{所有变量}}=0.073/0.261=0.0280
$$

F统计量的值0.28 落在 $F_{1,n-p-2}=F_{1,72}$ 分布的40%点处，对应的p值是0.60，因而重量不应该包含在模型中。

2.3 逐步选择程序

逐步选择程序是向前选择方法的一种改进。在向前选择中会出现这种情况，当新加入的变量加入到模型时，向前选择过程中已经加入的变量可能就显得不重要了，这在向前选择方法中是没有考虑的。逐步选择过程可以检验这种情况，方法是每一步在现有变量的基础上计算每个变量的部分平方和，执行偏F检验。如果模型中有一个变量不再是显著的，这个含有最小偏F统计的变狼就会被移出模型。当不再有变量加入或者移出模型时，结束过程并得到最终模型。

2.4 最优子集程序

对于预测变量集不是太大的数据集，最优子集是一种较好方法。但是如果预测变量超过30个，最优子集方法就会产生组合爆炸，难以控制。步骤如下：

分析人员需要指定需要多少个（假设为m）供筛选的模型，以及在一个模型中含有最大预测变量个数（假设为n）
对于含有一个预测变量的所有模型，例如：$y=b_0+b_1(糖),y=b_0+b_1(纤维)$,….等。计算对应的 $R^2$ ,修正 $R^2$ 和S值都计算出来，最优的m个模型是基于这些统计值得到。
对于含有两个最优的m个模型是基于这些统计值得到。
重复以上，直到达到最大的预测变量（n）个数，然后分析人员把预测变量个数为1,2,,..n的最优模型罗列，以选择最佳总体模型

实例，下图是最优子集程序用于谷物数据集的省略概览

[注意，整个过程比下图要复杂，例如变量数为1时，本应该有12行结果，下图中只简要用了两行，其他的也是]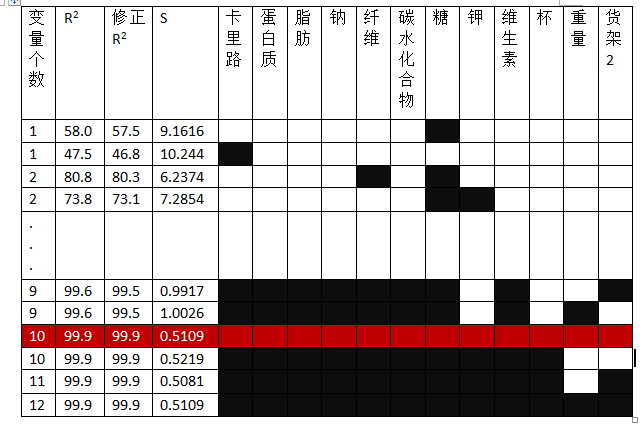

图中，每一行代表一个不同的模型，某模型中包含了哪个变量，该变量对应的方格被涂成黑色。如，第一个模型（第一行）仅包含了变量糖；第四个模型（第四行）包含了糖和钾。其中的最优模型子集被红色覆盖的那个模型（也即那一行）。

一 概念