一 问题描述
**如果我们有一组可见变量v,如何推断产生这些数据的模型m **
难点:除了可见变量v,通常还有一系列的隐含变量h,模型由1)
模型的类别ξ (如高斯分布,伽马分布,多项式分布等)与2)
模型的参数Θ 共同决定,即m (ξ, Θ ) 。
模型的选择 :假设 H为所有可能的模型集合(包括不同类别),那么选择m=argmax{p(m(ξ, Θ) |v ), m ∈ M},
上述问题的主要挑战在于计算p(h| v)或者计算在p(h| v)下的期望。
为什么做近似推断
概率推断的核心任务就是计算某分布下的某个函数的期望、或者计算边缘概率分布、条件概率分布等等。这些任务往往需要积分或求和操作,但在很多情况下,计算这些东西往往不那么容易。因为,
首先,积分中涉及的分布可能有很复杂的形式,这样就无法直接得到解析解;
其次,我们要积分的变量空间可能有很高的维度,这样就把我们做数值积分的路都给堵死了。
因此,进行精确计算往往是不可行的,需要引入一些近似计算方法。
二 近似推断的方法
2.1 随机方法
Gibbs采样法,通过大量的样本估计真实的后验,以真实数据为基础来近似目标分布。优点如下:
更精确;而且采样过程相对简单;易于操作,有着良好的理论收敛性,并且实现更加简单。但是收敛速度较慢,难以判断收敛程度的问题
2.2 确定近似法:变分法
用一些已知的简单的分布来近似后验分布。
优点: 有解析解、计算开销较小、速度快、易于在大规模问题中应用。
缺点:
推导过程相对复杂,对人的要求高,
推导出想要的形式比较困难,也就是说,这些简单的分布到底能多大程度生近似目标分布呢?很难衡量。
只是优化对应分布之间的KL散度得到最终的结果,变分下界小于等于目标函数,所以在近似分布难以拟合的时候,其结果是严格小于目标函数的。容易造成结果的不精确
三 近似后验分布学习
3.1 最大期望算法(EM算法)
概念: 期望最大算法是一种从不完全数据或有数据丢失的数据集(存在隐含变量)中求解概率模型参数的最大估计方法。
我们都知道似然估计,主要是用来估计未知参数$\theta$ ,通常我们已知服从某种分布的样本 $\lbrace x_1,x_2,…x_n\rbrace$。但是不知道样本参数$\theta$ 。 我们估计 $\theta$ 的思想是,取得使似然函数最大的 $\theta$。所谓的似然函数,即出现这一样本集合的概率函数:
$$
L(\theta) = \prod _{i=1} ^{n} p(x_i;\theta)
$$
其中的 $p_i$ 为每个样本出现的概率。累乘为同时出现的概率。
通常取对数,使连乘变累加。
$$
H(\theta) = ln(L(\theta)) =\sum _{i=1} ^n ln(p(x_i;\theta))
$$
最后求使得$H(\theta)$ 最大的 $\theta$ 值。通常是求导数,令导数为0,得到似然方程,解似然方程,得到的参数即为所求。
EM算法实际上与似然估计很相似,但有一条,就是它不能确定样本来自哪个分布(可能有好几个分布,这些分布产生的样本混合在一起,不能确定样本来自哪个分布)
所以EM算法比似然估计多了个过程就是,首先要估计样本来自哪个分布。
假设我们想估计知道A和B两个参数,在开始状态下二者都是未知的,但如果知道了A的信息就可以得到B的信息,反过来知道了B也就得到了A。可以考虑首先赋予A某种初值,以此得到B的估计值,然后从B的当前值出发,重新估计A的取值,这个过程一直持续到收敛为止。
算法流程:
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其极大似然估计值;
第二步是最大化(M),最大化在 E 步上求得的最大似然值来计算参数的值。
示例:已知200人的身高数据,性别未知,求不同性别的身高分布。
我们是先随便猜一下男生(身高)的正态分布的参数:如均值和方差是多少。例如男生的均值是1米7,方差是0.1米(当然了,刚开始肯定没那么准),然后计算出每个人更可能属于第一个还是第二个正态分布中的(例如,这个人的身高是1米8,那很明显,他最大可能属于男生的那个分布),这个是属于Expectation一步。有了每个人的归属,或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分,我们就可以根据之前说的最大似然那样,通过这些被大概分为男生的n个人来重新估计第一个分布的参数,女生的那个分布同样方法重新估计。这个是Maximization。然后,当我们更新了这两个分布的时候,每一个属于这两个分布的概率又变了,那么我们就再需要调整E步……如此往复,直到参数基本不再发生变化为止。
3.1.1 EM算法的推导过程
假设我们有一个样本集 $\lbrace x_1,x_2,…,x_m\rbrace。包含m个独立的样本。但是每个样本$i$对应的类别未知,也即隐含变量。故我们需要估计概率模型 $p(x,z)$ 的参数 $\theta$ ,但是由于里面包含了隐含变量z,所以很难用最大似然求解。但是如果知道Z,就很容易求解了。
对于参数估计,我们本质上还是想获得一个使似然函数最大化的那个参数$\theta$。现在与最大似然不同的只是似然函数式多了一个未知变量z。我们的目标变成找到合适的 $\theta$ 和 z,让$L(\theta)$ 最大。
$$
\sum _i log P(x^{(i)};\theta)= \sum _i log\sum _{z^{(i)}}P(x^{(i)},z^{(i)};\theta) \
\sum _i log _{z^{(i)}}Q_i (z^{(i)})\frac{P(x^{(i)}),z^{(i)}\theta}{Q_i(z^{(i)})} \
\ge \sum _i\sum _{z^{(i)}} Q_i (z^{(i)}) log\frac{P(x^{(i)}),z^{(i)}\theta}{Q_i(z^{(i)})}
$$
上式右边,第一行式子。这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和,也就得到等式左边为随机变量x的边缘概率密度
上式右边,第二行式子。只是分子分母同乘以一个相等的函数,还是有“和的对数”,无法求解。
上式右边,第三行式子。变成了“对数的和”,那这样求导就容易,此处的等号变为不等号源于Jense不等式。
3.1.2 Jensen不等式
如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X])
特别地,如果f是严格凸函数,当且仅当X是常量时,上式取等号。
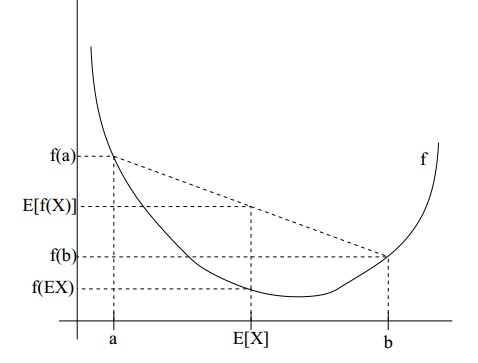
实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。(就像掷硬币一样)。X的期望值就是a和b的中值了,图中可以看到E[f(X)]>=f(E[X])成立。Jensen不等式应用于凹函数时,不等号方向反向。
回到EM算法推导的第二个式子,因为$f(x)=logx$ 为凹函数(其二次导数为 $-\frac{1}{x^2}<0$ 。式子中 $log _{z^{(i)}}Q_i (z^{(i)})\frac{P(x^{(i)}),z^{(i)}\theta}{Q_i(z^{(i)})}$ 是 $frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$的期望(考虑到 $E(x)=\sum x\star p(x))$ ,则$E(f(x))=\sum f(x)\starp(x)$ )。 而 $\sum_zQ_i(z^{(i)})=1 $
上式中,我们让 $Q_i$ 表示样本的隐含变量$z$ 的某种分布。$Q_i$满足的条件是 $\sum_z Q_i(z)=1,Q_i(z)\ge 0$。(如果z是连续性的,那么$Q_i$是概率密度函数,需要将求和符号换做积分符号)。比如要将班上学生聚类,假设隐藏变量z是身高,那么就是连续的高斯分布。如果按照隐藏变量是男女,那么就是伯努利分布了。
参考: